
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Момент импульса материальной точки относительно точки O определяется векторным произведением
|
|
|
|
Момент импульса материальной точки и тела. Момент силы. Второй закон Ньютона для вращательного движения материальной точки и тела. Условия равновесия абсолютно твердого тела.
Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:
 где × ‒ знак векторного произведения
где × ‒ знак векторного произведения
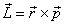 , где
, где  — радиус-вектор, проведенный из точки O,
— радиус-вектор, проведенный из точки O,  — импульс материальной точки.
— импульс материальной точки.
Момент импульса материальной точки относительно неподвижной оси Lz равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса Lx не зависит от положения точки O на оси z.
М = Fd — момент силы равен произведению величины силы на ее плечо.
Элементарная работа по повороту тела равна произведению момента силы на угол поворота.
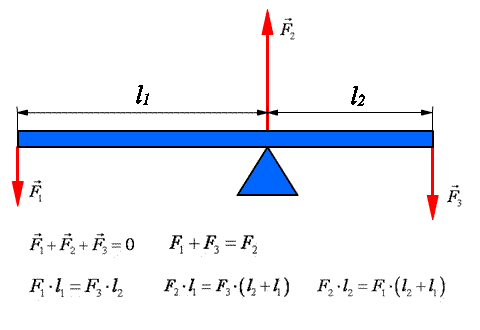
Итак, необходимые условия равновесия абсолютно твердого тела, имеющего неподвижную ось вращения: одновременное равенство нулю суммы сил и суммы моментов сил, действующих на тело.
Второй закон Ньютона для тела: угловое ускорение ε твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.
 (Эпселон и момент- векторные)
(Эпселон и момент- векторные)
Второй закон Ньютона для материальной точки: материальная точка может двигаться вокруг оси, оставаясь от нее на постоянном расстоянии, следовательно, ее траектория будет являться окружностью с центром на оси вращения. 
Это уравнение называется основным уравнением динамики вращательного движения. Итак, момент силы во вращательном движении играет такую же роль, как и сила в п
Вращательное движение. Момент инерции тела относительно оси. Теорема Штейнера. Момент силы относительно оси. Равноускоренное вращение.
Вращательное движение (тоже самое, что и вращение тела с неподвижной осью) — вид механического движения, при котором все точки тела (мы рассматриваем абсолютно твердое тело) описывают окружности, расположенные в параллельных плоскостях.
Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.
Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
 где:
где:
mi — масса i -й точки,
ri — расстояние от i -й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
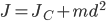 где: JC — известный момент инерции относительно оси, проходящей через центр масс тела;
где: JC — известный момент инерции относительно оси, проходящей через центр масс тела;
J — искомый момент инерции относительно параллельной оси;
m — масса тела;
 d — расстояние между указанными осями.
d — расстояние между указанными осями.
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Равноускоренное вращение — вращение с постоянным ускорением.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 863; Нарушение авторских прав?; Мы поможем в написании вашей работы!