Частотные критерии устойчивости

В основе частотных методов лежит принцип аргумента (следствие теоремы Коши относительно числа нулей и полюсов аналитической функции).

Проведем анализ свойств многочлена вида

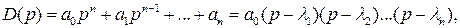
где 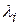– корни уравнения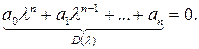

На комплексной плоскости рис. 4.44 каждому корню соответствует вполне определенная точка. Геометрически каждый корень 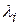можно изобразить в виде вектора, проведенного из начала координат в точку 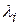: 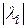– длина вектора, 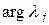– угол между вектором и положительным направлением оси абсцисс. Отобразим 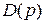в пространство Фурье, тогда где – элементарный вектор.

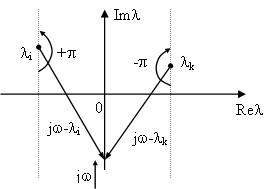
Рис. 4.44. Корни характеристического уравнения

на комплексной плоскости

Концы элементарных векторов находятся на мнимой оси: модуль вектора

,

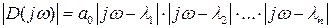а аргумент (фаза) –

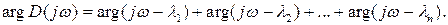
Направление вращения вектора против часовой стрелки принимают за положительное. Тогда при изменении w от до 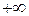каждый элементарный вектор 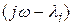повернется на угол +p, если 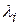лежит в левой полуплоскости.

Пусть 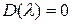имеет 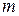корней в правой полуплоскости и 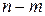– в левой, тогда при возрастании 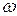от до 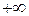изменение аргумента вектора 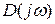(угол поворота 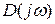, равный сумме изменений аргументов элементарных векторов)

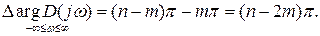
Изменение аргумента вектора 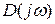при возрастании w от до 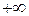равно разности 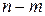корней уравнения 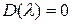, лежащих в левой части плоскости, и 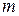корней уравнения, лежащих в правой части плоскости, умноженной на p.

Критерий Михайлова. Устойчивость замкнутой САУ определяется характеристическим полиномом

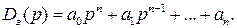
Согласно принципу аргумента для устойчивой системы

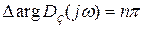, при .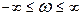

При изменении w от до 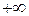вектор 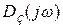на комплексной плоскости опишет своим концом кривую, которая называется характеристической кривой, или годографом вектора 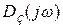(рис. 4.45):

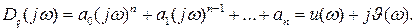
Можно показать, что функция 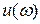– четная, а 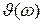– нечетная. Поэтому 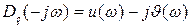, т.е. характеристическая кривая симметрична относительно действительной оси пр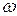и и . Отсюда следует, что угол поворота радиуса-вектора 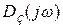на полусегментах (, 0] и [0, 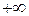) одинаков. Поэтому можно ограничиться построением характеристической кривой для положительных w, тогда 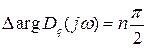, при .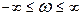

Система устойчива, если при изменении w от 0 до 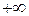годограф вектора 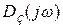(кривая Михайлова) обходит последовательно в положительном направлении 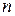квадратов.

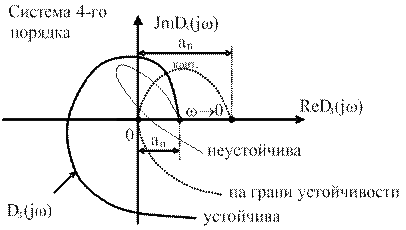
Рис. 4.45. Критерий Михайлова: – в статической

системе, 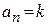– в астатической системе

Критерий Михайлова при инженерных расчетах используется сравнительно редко. По критериям Гурвица, Рауса и Михайлова можно судить об устойчивости САР как в замкнутом, так и в разомкнутом состояниях. С помощью критерия Михайлова, если система неустойчива, можно определить, сколько корней будет находиться в правой полуплоскости.

Если для устойчивой системы

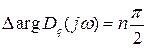, при ,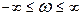

то для неустойчивой системы

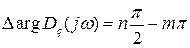, при .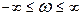

Например, система 4-го порядка, кривая Михайлова которая обозначена (1) на рисунке, имеет два корня с положительной вещественной частью, так как

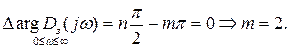
В статической системе выбирают на 30% меньше критического значения.

Критерий Найквиста. Критерий базируется на частотных характеристиках разомкнутой цепи системы автоматического управления, так как по виду частотных характеристик разомкнутой цепи можно судить об устойчивости замкнутой системы.

Критерий Найквиста нашел широкое применение в инженерной практике по следующим причинам:

1. Устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой цепи, а эта функция чаще всего состоит из простых сомножителей. Коэффициентами передаточной функции являются реальные параметры системы, что позволяет выбрать их из условий устойчивости.

2. Для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы (объект регулирования, исполнительный орган), что повышает точность полученных результатов.

3. Исследовать устойчивость можно по ЛЧХ, построение которых несложно.

4. Удобно определять устойчивость системы.

Система, устойчивая в разомкнутом состоянии. Этот случай соответствует системам автоматического управления без астатизма. Пусть

.

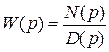Введем вспомогательную функцию

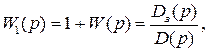
заменим , и тогда

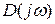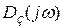Согласно принципу аргумента изменение аргументов и при 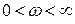равно 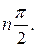Тогда 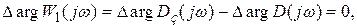т.е. годограф 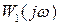не должен охватывать начало координат.

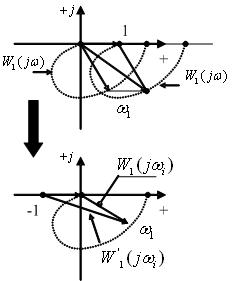
Рис. 4.46. Годограф состояния системы

Для упрощения анализа и расчетов сместим начало радиуса-вектора из начала координат в точку 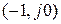, а вместо вспомогательной функции W₁(jw) используем АФХ разомкнутой системы W(jw).

Формулировка критерия: если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку 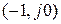(рис. 4.47).

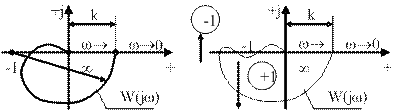
Рис. 4.47. Разность числа положительных и отрицательных переходов АФХ левее точки 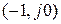равно нулю

Система, имеющая полюсы на мнимой оси в разомкнутом состоянии. Характеристический многочлен разомкнутой системы имеет нулевые и (или) чисто мнимые корни (имеются нулевые полюса передаточной функции разомкнутой системы), остальные корни лежат в левой полуплоскости, т.е. в разомкнутом состоянии система является нейтрально-устойчивой:

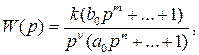
где 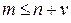– соответствует астатической системе; 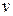– порядок астатизма системы.

В этом случае АФХ разомкнутой системы будет иметь разрыв непрерывности в точке w=0. В этой точке модуль 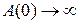, а фаза делает скачок на 180° (при n=1). Для получения определенности в ходе АФХ необходимо отнести нулевой корень знаменателя передаточной функции W(p) либо к левой, либо к правой полуплоскостям корней. Первое является более удобным, так как при этом все корни знаменателя 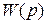будут расположены в левой полуплоскости.

Обойдем корень 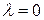по полуокружности бесконечно малого радиуса так, чтобы корень остался слева. При движении по этой полуокружности против часовой стрелки независимая переменная 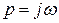меняется по закону где 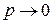представляет собой радиус полуокружности, а j - аргумент, меняющийся от -p/2 до +p/2. При этом передаточная функция W(p) может быть представлена в ви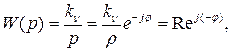де где 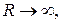а аргумент меняется в пределах от +p/2 до -p/2.

Таким образом, во время движения по полуокружности бесконечно малого радиуса передаточная функция может быть представлена в виде вектора бесконечно большой длины, поворачивающегося на комплексной плоскости по часовой стрелке на угол, равный p (от p/2 до -p/2), что соответствует полуокружности бесконечно большого радиуса.

При n=2 вектор бесконечно большой длины поворачивается по часовой стрелке на угол 2p.

Так же, как и при n=1, здесь можно получить условную устойчивость, колебательную границу устойчивости и неустойчивость.

Из рис. 4.49 следует, что абсолютная устойчивость может быть получена при n£2, при n³3 - только условная устойчивость. Абсолютно устойчивой называют систему, которая сохраняет устойчивость при любом уменьшении коэффициента усиления разомкнутой цепи, иначе система – условно устойчивая.

Изложенный выше прием используют и при мнимых корнях.

Для анализа устойчивости системы АФХ дополняют окружностью бесконечно большого радиуса при w®0 против часовой стрелки до положительной вещественной полуоси, а в случае чисто мнимых корней - полуокружностью по часовой стрелке в точке разрыва непрерывности АФХ.

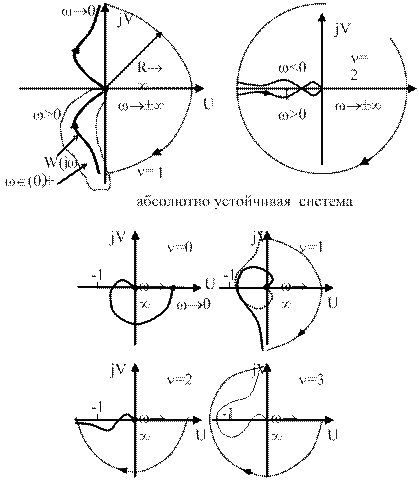
Рис. 4.49. Примеры АФХ устойчивых систем

автоматического управления

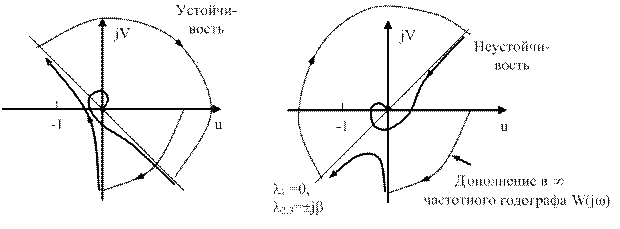
а б

Рис. 4.50. Анализ устойчивости системы АФХ

Система с неустойчивой разомкнутой цепью. Более общий случай - знаменатель передаточной функции разомкнутой системы с любой степенью астатизма содержит корни, лежащие в правой полуплоскости. Появление неустойчивости разомкнутой системы вызывается двумя причинами:

1) следствием наличия неустойчивых звеньев;

2) следствием потери устойчивости звеньев, охваченных положительной или отрицательной обратными связями.

Следует заметить, что, хотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным и его надо избегать, стремясь использовать только устойчивые местные обратные связи. Это объясняется наличием некоторых нежелательных свойств, в частности появлением условной устойчивости, которая при имеющихся в системе нелинейностях может в некоторых режимах привести к потере устойчивости и появлению автоколебаний. Поэтому, как правило, при расчете системы выбирают такие местные обратные связи, которые были бы устойчивыми при разомкнутой главной обратной связи.

Пусть характеристический многочлен D(p) разомкнутой системы имеет m корней с положительной вещественной частью.

Тогда 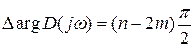, при 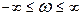. Вспомогательная функция 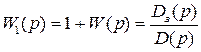при замене согласно принципу аргумента для устойчивых замкнутых систем должна иметь следующее изменение аргумента при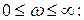

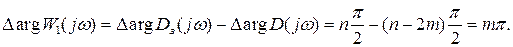
Дата добавления: 2014-12-26