Анализ случайных процессов при срыве управления

Этот анализ касается рассмотрения более общего случая, когда нужно учитывать наличие в системе случайных начальных условий (начальных зарядов или токов на накопительных элементах, а также их производных до n-1 порядка включительно). Эти начальные условия в данном случае соответствуют моменту срыва. Именно в момент срыва те заряды или токи и их производные, которые имели место в схеме, являются начальными для процессов, которые начинают развиваться в схеме после срыва.

В общем случае исследуемый процесс 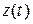и случайное возмущение 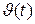в линейной системе (рис. 5.3) связаны стохастическим дифференциальным уравнением вида

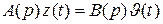
или

,

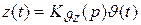где 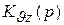— операторный коэффициент передачи системы для 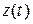по отношению к возмущению 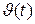; 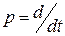— оператор дифференцирования.

Дифференциальные операторы 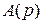и 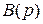обычно (см. подразд. 2.5) записывают в виде полиномов от оператора р:

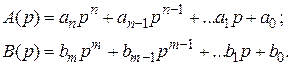
Применительно к рассмотренной выше обобщенной замкнутой системе функция 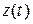представляет собой процесс, исследуемый в любой заданной для изучения точке этой системы. В частности, процессом 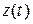является ошибка x(t) или выходной процесс y(t). Например, уравнение (5.30) может быть приведено к выражению (5.29):

,

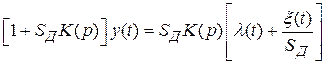где ; .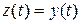

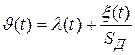Аналогичное уравнение для 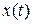(4.5) имеет вид

,

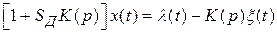где 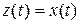, а .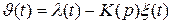

Очевидно, что в одной и той же системе различным процессам 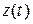и 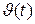соответствуют разные операторы 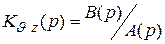. Так, в рассмотренной обобщенной схеме для 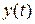и 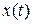по отношению к 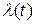и 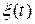операторные коэффициенты передачи имеют вид (4.4), (4.6), (4.7). Например, для фильтра нижних частот (см. рис. 4.9, а) с коэффициентом передачи

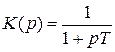
динамическая ошибка

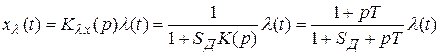
или

.

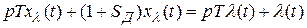Подставляя в полученное выражение формально 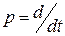, получаем дифференциальное уравнение

.

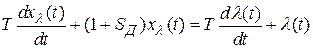Аналогично для флуктуационной ошибки

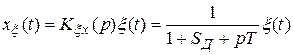
запишем дифференциальное уравнение

.

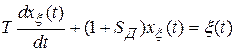Случайные процессы 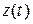и 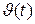в формуле (5.29) можно представить в виде суммы их математических ожиданий и центрированных случайных составляющих:

,

,

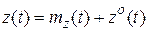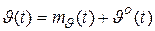где функци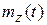и и 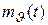в дальнейшем будем полагать детерминированными. Математические ожидания процессов 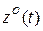и 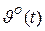в силу их центрированности равны нулю, т.е. , 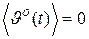. Так как операторы 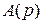и 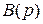линейны, то уравнение (5.29) распадается на два независимых уравнения:

,

.

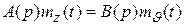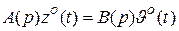Таким образом, линейная система может быть исследована для регулярных и случайных процессов раздельно (при исследовании одного процесса, другой можно полагать равным нулю). На конечном этапе исследования результаты складываются алгебраически.

Для рассмотренной обобщенной схемы, как видно из уравнений (5.30), (5.32), (5.39), (5.40), в предположении, ч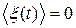то , то

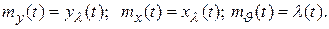
Решения уравнений (5.41), (5.42) находим в виде двух слагаемых:

,

.

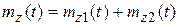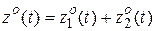Первые слагаемые характеризуют процессы, вызванные внешним воздействием 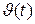при нулевых начальных условиях (частные решения дифференциальных уравнений), вторые — обусловлены начальными условиями, т.е. зарядами накопительных элементов схемы, и представляют собой свободные движения в системе, не связанные с внешним воздействием .

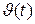В дальнейшем при исследовании того или иного случайного процесса z(t) будем предполагать его нормальным. Как известно, исчерпывающие характеристики нормального процесса – математическое ожидание, корреляционная функция и, в частности, дисперсия. Такое предположение оправданно, так как даже в том случае, если процесс не является нормальным, при прохождении его через узкополосную систему он в значительной степени «нормализуется».

В связи с тем, что дифференциальное уравнение (5.29) распадается на систему двух дифференциальных уравнений (5.41), (5.42), в результате их анализа достаточно найти из первого уравнения 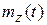, а из второго — корреляционную функцию процесса 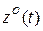. Первое уравнение решается известными методами теории линейных дифференциальных уравнений с постоянными коэффициентами.

Для определения корреляционной функции 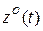целесообразно воспользоваться либо методом импульсных характеристик, либо методом преобразований Фурье (для первого слагаемого) и известными методами нахождения общего решения дифференциального уравнения (для второго слагаемого).

Корреляционная функция процесса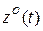

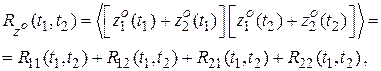
где 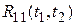– корреляционная функция процесса 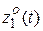; 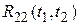– корреляционная функция процесса 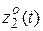; 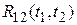и 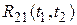– взаимные корреляционные функции процессов 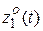и 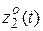. Дисперсия находится из корреляционной функции для совпадающих моментов времени:

.

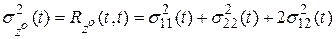Можно показать, что в переходном режиме, т.е. по истечении сравнительно небольшого промежутка времени с момента подачи входного возмущения 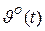, корреляционная функция 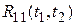определяется формулой

,

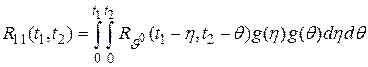где 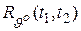— корреляционная функция входного воздействия 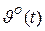, которое полагается нормальным стационарным случайным процессом

,

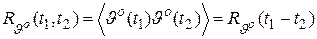g(t) — функция отклика системы на «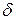 -импульс»,

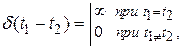
называемая импульсной характеристикой (весовой функцией, аппаратной функцией и др.). Эта функция может быть найдена либо с помощью обратного преобразования Лапласа от операторного коэффициента передачи

,

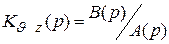либо с помощью преобразования Фурье при постановке .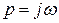

Для совпадающих моментов времени корреляционная функция представляет собой дисперсию случайного процесса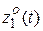

.

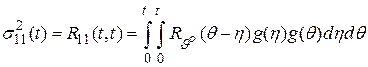В установившемся режиме, т.е. по истечении достаточно большого промежутка времени с момента включения входного возмущения 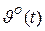, положим 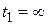и 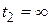в верхних пределах интегрирования и перейдем от функции 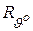и g к их преобразованиям Фурье. Тогда

,

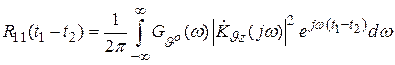где 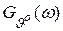– энергетический спектр случайного процесса .

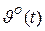Соответственно дисперсия

.

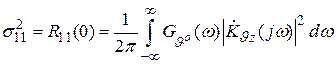Если корреляционная функция процесса 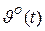равна ( 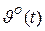– белый шум)

,

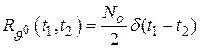то в переходном режиме дисперсию (5.51) получим из выражения

,

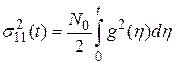где 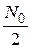— энергетический спектр случайного процесса 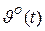(белого шума). В установившемся режиме корреляционная функция (5.52) с учетом выражения (5.54) имеет следующий вид:

.

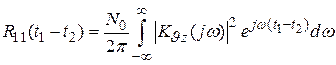Дисперсия в этом случае

.

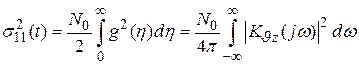Корреляционная функция 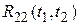относится к процессу 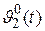, который обусловлен случайными начальными условиями. Следует отметить, что при заданных начальных условиях процесс 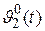детерминирован и определяется характером элементов схем в замкнутой системе и связей между ними. Если начальное условие – это напряжение заряда конденсатора в схеме, то 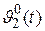- детерминированная функция, связанная с его разрядом. Случайность функции 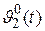проявляет себя лишь при многократных повторениях процессов регулирования при случайных значениях начальных условий, вызванных наличием в схеме случайных процессов и 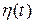. Корреляционная функция 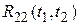находится путем усреднения произведения 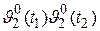по всем возможным случайным начальным условиям:

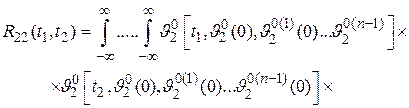
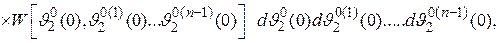
где 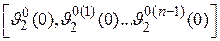— начальные значения функции 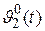и ее производных; 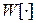— совместная плотность вероятности этих значений. Для нахождения дисперсии 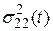необходимо вычислить выражение (5.58) для совпадающих моментов времени, т.е. положить .

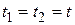Более сложным являются выражения для взаимно корреляционных функци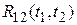й и 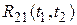. Однако при дельта-коррелированном входном случайном возмущении эти функции равны нулю:

.

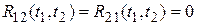В этом случае

,

.

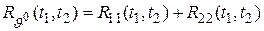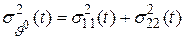В дальнейшем будем полагать, что при нормальном регулировании в замкнутой системе все ее накопительные элементы разряжены, т.е. все начальные условия нулевые до момента подачи входных возмущений (или включения системы). Начальные условия учитываем лишь при исследовании процессов, возникающих при срыве регулирования. Это те значения процессов и их производных, которые были зафиксированы в схеме в момент срыва.

Наличие случайных возмущений ухудшает память замкнутой системы. Для расчета вероятности (5.2) необходимо определить дисперсию флуктуационной ошибки 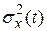. Эта дисперсия может быть вычислена по формулам (5.47), (5.55), (5.57) и (5.58) для 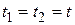. Например, для системы с пропорционально интегрирующим фильтром и интегратором при воздействии на нее белого шума дисперсия ошибки может быть приближенно вычислена по формуле [1]

,

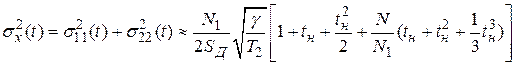где 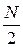и 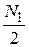— спектральные плотности процессов 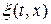и 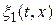на частоте 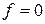; 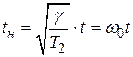– нормированное время.

Расчет дисперсии показывает, что ее величина в течение некоторого периода времени увеличивается, причем скорость роста уменьшается с увеличением постоянной времени 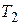и снижением 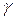, что улучшает память системы. Однако при этом снижается ее быстродействие (5.62).

Дата добавления: 2014-12-26