
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Устойчивость в линейных автоматических системах
|
|
|
|
Автоматическая система управления должна сохранять работоспособность при воздействии на нее регулярных или случайных шумовых составляющих. Линейная система называется устойчивой, если при выведении ее внешними воздействиями из состояния равновесия она возвращается в него после прекращения этого воздействия (рис. 4.43). Кривые 1 и 2 характеризуют устойчивую систему, кривые 3 и 4 – системы неустойчивые, а системы 5 и 6 находятся на границе устойчивости: 5 – нейтральная система, 6 – колебательная система. Если система неустойчива, то она не возвращается в исходное состояние при окончании внешнего воздействия.
Система автоматического управления устойчива, если абсолютная величина отклонения регулируемой функции, получившаяся в результате возмущающего воздействия, по истечении достаточно большого промежутка времени после прекращения действия возмущения становится меньше наперед заданного значения 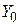 , т.е.
, т.е. 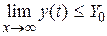 .
.
Линейная система управления в общем случае описывается линейным дифференциальным уравнением с постоянными коэффициентами и в операторной форме определяется выражением
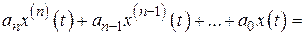
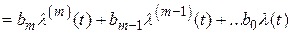 . (4.93)
. (4.93)
Решение дифференциального уравнения (движение системы) состоит из двух частей:
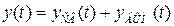 ,
,
где 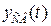 – решение однородного уравнения,
– решение однородного уравнения, 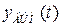 – частное решение неоднородного уравнения, зависящее от входного воздействия
– частное решение неоднородного уравнения, зависящее от входного воздействия 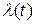 на систему.
на систему.
 |
а б
Рис. 4.43. Поведение системы при воздействии возмущения c момента времени t1 по t2: а – устойчивые системы 1,2, неустойчивые системы 3,4; б – нейтральные системы на грани устойчивости (5,6)
Система может совершать движения за счет внешнего воздействия и начальных условий: за счет начальных условий – свободное движение, затухающие в устойчивых системах, за счет внешнего воздействия – вынужденное движение.
Устойчивость системы определяется решением однородного дифференциального уравнения
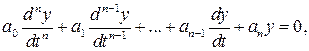
решение которого имеет вид
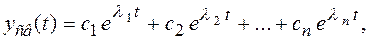
где 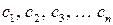 – постоянные интегрирования, определяемые из начальных условий,
– постоянные интегрирования, определяемые из начальных условий, 
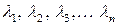 – корни характеристического уравнения;
– корни характеристического уравнения;
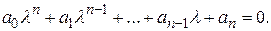
Корни характеристического уравнения не зависят ни от вида возмущения, ни от начальных условий, а определяются только коэффициентами 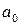 ,
, 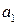 ,
, 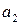 ,…,
,…, 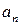 , т.е. параметрами и структурной системой.
, т.е. параметрами и структурной системой.
Вынужденная составляющая 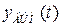 , зависящая от вида внешнего воздействия и правой части дифференциального уравнения (4.93), на устойчивость не влияет.
, зависящая от вида внешнего воздействия и правой части дифференциального уравнения (4.93), на устойчивость не влияет.
Состояние равновесия системы при различных значениях корней характеристического уравнения представлено в табл. 4.1.
1. Если корни характеристического уравнения вещественные и неравные и среди корней имеется хотя бы один положительный корень li, то соответствующее слагаемое 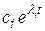 - возрастающая экспонента, и весь процесс будет расходящимся.
- возрастающая экспонента, и весь процесс будет расходящимся.
2. Если характеристическое уравнение имеет пару мнимых сопряженных корней 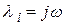 и
и 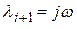 , а остальные корни вещественные и отрицательные, то в этом случае решение
, а остальные корни вещественные и отрицательные, то в этом случае решение 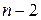 слагаемых – затухающие экспоненты вида
слагаемых – затухающие экспоненты вида 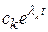 , пара мнимых корней соответствует двум слагаемым
, пара мнимых корней соответствует двум слагаемым 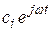 и
и 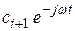 . Пользуясь формулой Эйлера, напишем следующие равенства:
. Пользуясь формулой Эйлера, напишем следующие равенства:
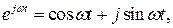
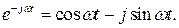
Следовательно,
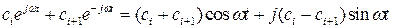 ,
,
где 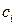 и
и 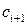 - комплексно сопряженные числа, поэтому
- комплексно сопряженные числа, поэтому 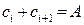 и
и 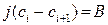 являются вещественными числами. Тогда
являются вещественными числами. Тогда
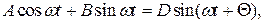
где 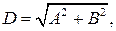
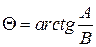 .
.
Решение однородного дифференциального уравнения будет иметь вид 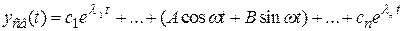 – незатухающие и нерасходящиеся гармонические колебания.
– незатухающие и нерасходящиеся гармонические колебания.
Таблица 4.1
| Корни характеристи-ческого уравнения | Слагаемое свободного решения | График функции члена решения | Примечание | |||
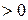 , действитель-ные , действитель-ные
|
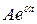
| 
| 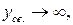 система неустойчивая система неустойчивая
| |||
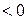 , действитель-ные , действитель-ные
|
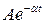
| Данный член стремится к нулю | ||||
| =0 |
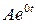
| 
| Система неустойчивая; возможно, нейтральная | |||
| Два нулевых корня |
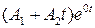
| 
| Система неустойчивая | |||
| Корни комплексные, действительная часть положительная |
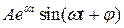
| 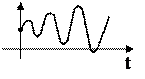
| Система неустойчивая | |||
| Корни комплексные, действительная часть отрицательная |
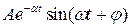
|
| Возможно, система устойчивая | |||
| Корни мнимые сопряженные |
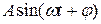
| 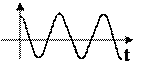
| Система неустойчивая; возможно, на грани устойчивости |
3. Пусть характеристическое уравнение имеет пару комплексных сопряженных корней 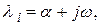
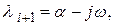 остальные корни – вещественные отрицательные. В этом случае
остальные корни – вещественные отрицательные. В этом случае
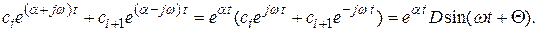
Если вещественная часть комплексных корней отрицательна, то 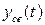 - затухающая функция.
- затухающая функция.
4. Если характеристическое уравнение имеет нулевой корень 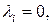 тогда
тогда 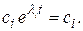 Если все остальные корни имеют отрицательные вещественные части или отрицательны, то
Если все остальные корни имеют отрицательные вещественные части или отрицательны, то
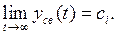
5. Если характеристическое уравнение имеет кратные корни, то при m кратных вещественных корней 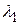
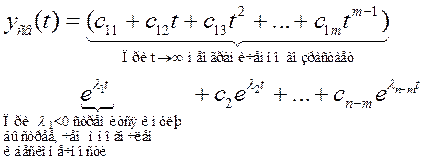
Составляющая 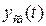 для кратных корней стремится к 0 при
для кратных корней стремится к 0 при 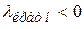 . Если остальные корни – с отрицательными вещественными частями или отрицательны, то
. Если остальные корни – с отрицательными вещественными частями или отрицательны, то 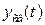 – сходящаяся функция.
– сходящаяся функция.
В устойчивых системах автоматического регулирования все корни характеристического уравнения должны лежать в комплексной плоскости корней слева от мнимой оси.
Эти выводы справедливы для линеаризованных уравнений, полученных в результате отбрасывания всех членов разложения в ряд Тейлора, содержащих отклонения координат в степени выше первой.
Линеаризованные уравнения названы А.М. Ляпуновым уравнениями первого приближения.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 735; Нарушение авторских прав?; Мы поможем в написании вашей работы!
