Примеры расчетов дисперсий флуктуационных ошибок

Эквивалентная шумовая полоса

В выражении (4.70) для дисперсии интеграл, определяющий площадь под функцией 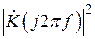, можно записать таким образом:

,

где 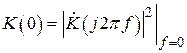; 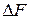– основание эквивалентного прямоугольника, площадь которого равна интегралу от функции .

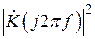Обычно 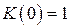. Тогда

.

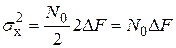Это простейшая, но очень важная инженерная формула для расчета дисперсии помехи. Величину 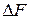часто называют эквивалентной шумовой полосой пропускания системы (фильтра).

1. Флуктуационная ошибка в замкнутой системе с инерционным звеном в качестве фильтра нижних частот.

Флуктуационную ошибку, которую принято характеризовать дисперсией 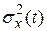в установившемся режиме, т.е. при 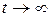, находим по выражению (4.71)

.

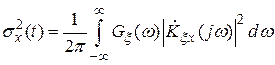При условии, что шумовой процесс 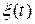в схеме (см. рис. 4.40), является 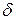-коррелированным, т.е энергетический спектр 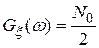, дисперсия флуктуационной ошибки

,

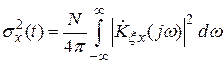где 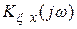находится с учетом выражений (4,7), (4.79) аналогично уравнению (4.71):

.

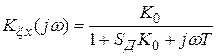Тогда

.

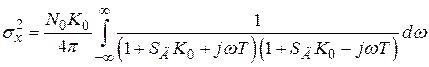Интегралы типа (4.78), (4.79), а следовательно, и (4.80) могут быть решены путем использования формул-шаблонов. Для этого необходимо их представить в виде выражения (4.73). Для формулы (4.73) :

,

,

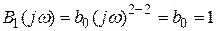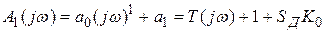т.е. , , .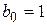

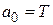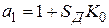Следовательно,

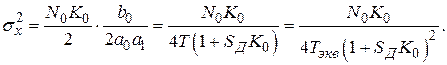
Анализируя выражение, приходим к выводу, что дисперсия флуктуационной ошибки уменьшается с увеличением постоянной времени Т,которая характеризует быстродействие системы.

Из сравнения выражений (4.27) и видно, что при повышении быстродействия системы путем уменьшения Т уменьшается динамическая ошибка, но при этом растет флуктуационная, и наоборот. Это общая закономерность следящих систем.

2. Флуктуационная ошибка в замкнутой системе с одним интегратором в качестве фильтра нижних частот.

Для этой флуктуационной ошибки

,

,

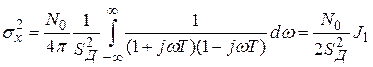где

, , .

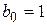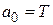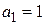Тогда

.

Сравнивая выражения (4.27) и (4.82), также видим, что повышение быстродействия системы, т.е. уменьшение величины 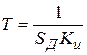, приводит к уменьшению динамической ошибки и увеличению флуктуационной.

3. Флуктуационная ошибка в замкнутой системе с последовательно включенными пропорционально интегрирующим фильтром и интегратором.

Для нее коэффициент передачи (4.28) определяется так:

.

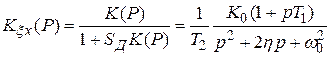Тогда для белого шума 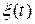в соответствии с выражением (4.79)

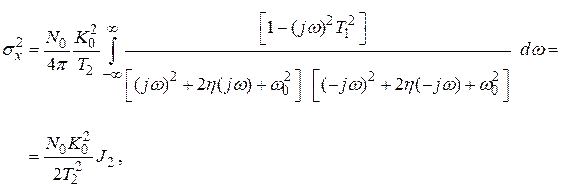
где ; ; ; ; .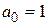

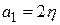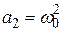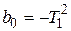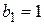Подставив эти значения в формулу для 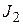(4.75), получим

.

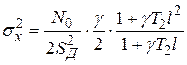Графики зависимостей 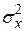от 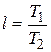приведены на рис. 4.40.

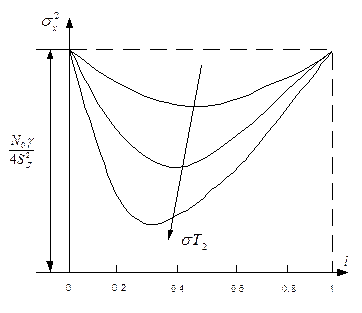
Рис. 4.40. Зависимость дисперсии от отношения постоянных времени

Из этих графиков видно, что для каждого значения 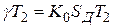существуют оптимальные значения отношений постоянных времен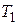и и 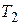, которые можно найти, продифференцировав по 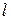выражение (4.84) и приравняв производную к нулю. В результате этого получим

.

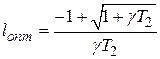При значениях 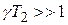, что обычно выполняется на практике и характерно для высокого коэффициента усиления 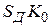в замкнутой цепи:

; .

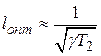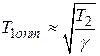4. Флуктуационная ошибка в замкнутой системе с последовательно включенными двумя интеграторами и стабилизирующим звеном.

Для определения флуктуационной ошибки в этой системе воспользуемся результатами анализа системы с пропорционально интегрирующим фильтром.

Переход к этой схеме от схемы пропорционально интегрирующего фильтра можно осуществить, положив .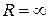

Тогда дисперсию ошибки получим, подставив в выражение (4.84) 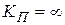и :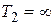

.

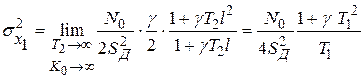Так же, как и для системы с инерционным звеном и интегратором, можно показать, что динамическая и флуктуационная ошибки находятся в противоречии: при уменьшении величины одной ошибки увеличивается величина второй. Это объясняется тем, что, стремясь уменьшить динамическую ошибку, повышают быстродействие системы (например, путем увеличения 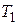, , 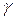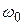). Однако при этом увеличивается полоса пропускаемых частот, что при широкополосном шуме приводит к росту дисперсии.

Дата добавления: 2014-12-26