Основные статистические характеристики случайных процессов

Наиболее широко используемыми статистическими характеристиками случайного процесса являются математическое ожидание, дисперсия и корреляционная функция.

Математическое ожидание (среднее значение)

.

Знак обозначает операцию статистического усреднения, – плотность вероятности случайного процесса 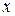в момент времени .

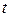Дисперсия

,

где – центрированная случайная функция, математическое ожидание которой .

Корреляционная функция

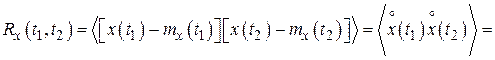
где 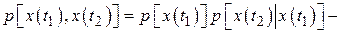совместная плотность вероятности значений 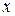в моменты врем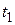ени и ,
– условная плотность вероятности, величина которой зависит от степени статистической связи значений 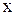в моменты времен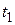и и 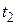. Корреляционная функция в совпадающие моменты времени 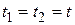равна дисперсии 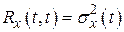, а дисперсия является максимальным значением корреляционной функции. По мере удаления момента времени 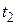от момента времени 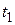степень зависимости 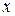в момент времени 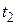от 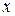в момент времени 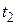, как правило, уменьшается.

Предположим, что случайные значения величины 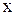в моменты времен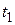и и 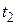– независимы. Тогда

и

.

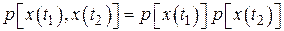При этом предположении двойное интегрирование в (4.48) сводится к повторному:

Выражение справа равно произведению математических ожиданий центрированных случайных процессов и равно нулю

.

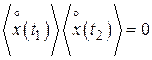Так как по мере удаления момента времени 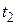от момента 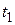степень статистической связи случайных величин и в большинстве случаев будет убывать, то корреляционная функция будет иметь спадающий характер. Максимальное значение она имеет в точках (связь максимальна). Типичные формы корреляционных функций приведены на рис. 4.29.

Рис. 4.29. Типичные формы корреляционных функций

Корреляционные функции для двух случайных процессов и 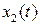(рис. 4.30) представлены на рис. 4.31.

а	б
Рис. 4.30. Примеры случайных процессов и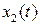
а	б
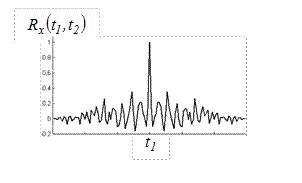
Рис. 4.31 Корреляционные функции: а – для процесса ; б – для процесса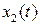

Процесс, показанный на рис. 4.30, а, имеет более узкую корреляционную функцию, так как визуально видно, что связь величин и 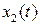по мере увеличения для первой функции будет уменьшаться быстрее.

Классификация случайных процессов

В простейшем случае различают такие случайные процессы:

1) стационарные и нестационарные;

2) гауссовские и негауссовские;

3) эргодические и неэргодические.

У стационарных процессов математическое ожидание , дисперсия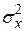

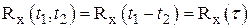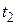не изменяются во времени, т.е. и . Корреляционная функция для стационарных процессов зависит только от разности аргументов . Последнее означает, что где бы мы не взяли на оси времени моменты и , степень связи в среднем и 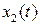будет определяться лишь взаимным расстоянием 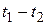или (рис. 4.32).

При 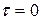корреляционная функция имеет максимальное значение и равна дисперсии. По мере увеличения разности значение корреляционной функции уменьшается.

  Рис. 4.32. Стационарный случайный процесс

На рис. 4.33 - 4.34 показаны примеры нестационарных случайных функций.

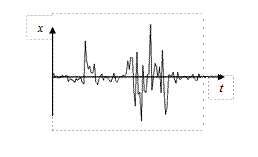а	б
Рис. 4.33. Примеры нестационарных процессов: а – 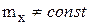, , 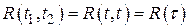; б – , ,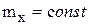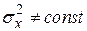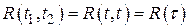

Рис. 4.31. Нестационарный процесс с параметрами , ,

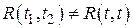
Гауссовские процессы отличаются от негауссовских тем, что у первых в каждом сечении 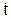плотности вероятности имеют нормальный (гауссовский) закон распределения вероятности (рис. 4.36)

.

Рис. 4.36. Гауссовский процесс

Гауссовские процессы могут быть как стационарными, так и нестационарными.

Особенно необходимо подчеркнуть, что для полного статистического описания гауссовских процессов достаточно знать их математические ожидания и корреляционную функцию , для стационарного случайного процесса корреляционная функция вырождается в дисперсию , как это видно из (4.50).

Эргодический процессы – это стационарные случайные процессы, статистические характеристики которых можно определить, заменяя усреднение по ансамблю реализаций на усреднение по времени для одной теоретически бесконечно длинной реализации.

Т.е. математическое ожидание, дисперсия и корреляционная функция могут быть получены по одной бесконечно длинной реализации и примут вид

,

,

.

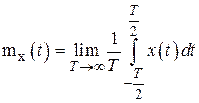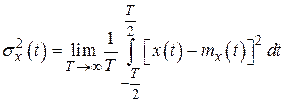Если оценка корреляционной функции осуществляется на конечном интервале, то

,

.

Если ширина корреляционной функции намного меньше интервала 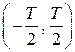, то

.

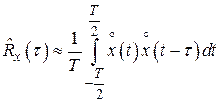Согласно приведенной классификации во всем множестве случайных процессов вместо рассмотренных процессов можно проиллюстрировать подмножествами, показанными на рис. 4.37.

Рис. 4.37. Множество случайных процессов

Дата добавления: 2014-12-26