Анализ замкнутой системы с последовательно включенными пропорционально-интегрирующим фильтром и интегратором

Схема замкнутой системы с последовательно включенными пропорционально-интегрирующим фильтром и интегратором системы показана на рис. 4.18. Шум .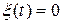

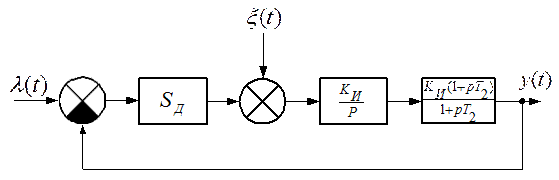
Рис. 4.18. Замкнутая система с интегратором и пропорционально- интегрирующим фильтром

Передаточная характеристика фильтра

,

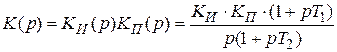где — передаточная характеристика пропорционально-интегрирующего фильтра. Разновидности схем пропорционально-интегрирующих фильтров изображены на рис. 4.19.

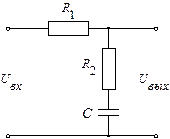
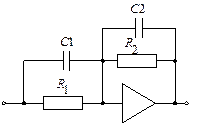
а б в

Рис. 4.19. Схемы пропорционально-интегрирующих фильтров

Для этих схем постоянные времени равны:

а) , , ;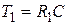

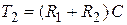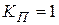б) , , ;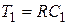

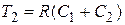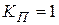в) , , .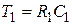

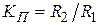Например, для схемы (рис. 4.19, а)

.

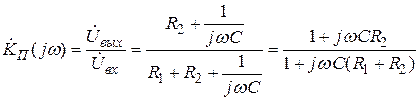Переходная и частотная характеристики пропорционально интегрирующего фильтра показаны на рис. 4.20.

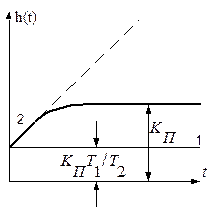
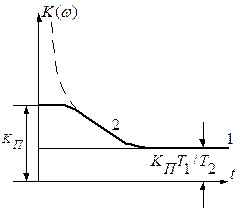
а б

Рис. 4.20. Переходная и частотная характеристики пропорционально- интегрирующего фильтра

На этих характеристиках участки I свойственны пропорциональной передачи напряжения со входа на выход, а участки 2 — интегрирующим звеньям .

Для нахождения динамической ошибки подставим формулу (4.28) в (4.18). Тогда дифференциальное уравнение примет вид

,

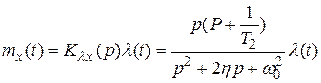где 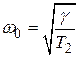— собственная частота замкнутой системы; 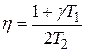— затухание;

, .

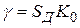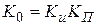Дифференциальное уравнение в естественном виде можно получить, избавляясь от знаменателя в (4.29) и формально подставляя в него :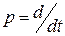

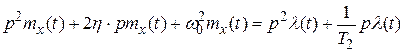
или

.

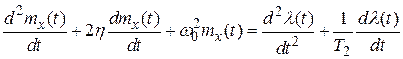Изображение ошибки 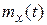при входном воздействии в виде единичного скачка определяется выражением

,

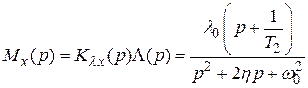где 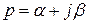, а соответствующий изображению оригинал, т.е. ошибка 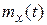, найденная по справочным таблицам, будет равна

В первой строке формулы (4.32) учитывается, что дискриминант 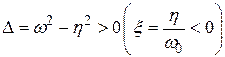, где 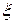- коэффициент демпфирования. В средней формуле – 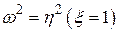. В нижней строчке этой формулы .

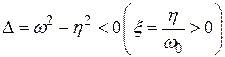Графики зависимостей (4.32), а также входного процесса 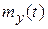показаны на рис. 4.21.

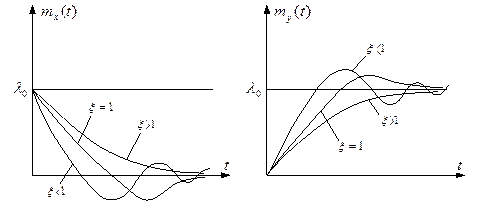
а б

Рис. 4.21. Зависимости 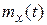, 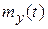для системы с пропорционально- интегрирующим фильтром и интегратором

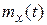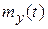Как видно из этих графиков, процессы установления и при 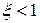носят колебательный характер, т.е. в этом случае в системе существует перерегулирование.

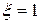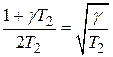При критическом значении :

или ,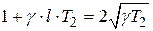

где .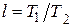

Графики зависимостей динамической ошибки от времени в критическом режиме, т.е. при 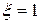, для различных значений 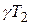изображены на рис. 4.22.

Рис. 4.22. Поведение динамической ошибки в критическом режиме

при различных значениях

Из этих графиков видно, что с ростом 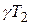скорость уменьшения динамической ошибки увеличивается, однако при этом, хотя и незначительно, увеличивается перерегулирование.

При 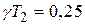, как нетрудно видеть из (4.33), пропорционально- интегрирующий фильтр вырождается в инерционное звено.

Время установления выходного процесса 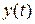является временем уменьшения ошибки до уровня 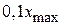и примерно равно (см. рис. 4.22):

.

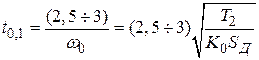При подаче на вход воздействия, изменяющегося по линейному закону

,

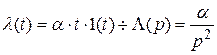изображение ошибки 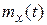равно

.

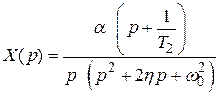Тогда ошибка при коэффициенте демпфирования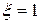

.

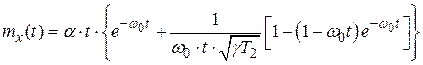Графики зависимостей ошибки 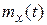и выходного воздействия показаны на рис. 4.23.

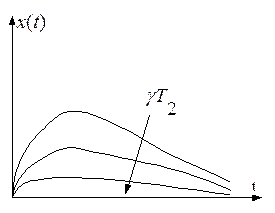
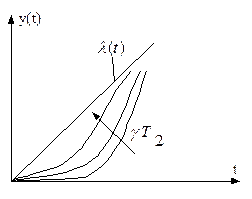
Рис. 4.23. Зависимости динамической ошибки и выходного процесса

при линейно изменяющемся воздействии

Так как система имеет астатизм первого порядка, то для единичного скачка, математически описываемого выражением (4.20) из (4.33), следует 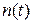, а для воздействия (4.35) из (4.37) ошибка стремится к постоянной величине:

.

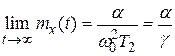При воздействии 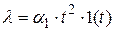ошибка со временем будет увеличиваться.

Дата добавления: 2014-12-26