Понятие астатизма системы управления

Понятие астатизма системы позволяет установить, в каких случаях и при каких сигналах динамическая ошибка слежения будет стремиться или не стремиться к нулю.

Входные воздействия в схемных моделях систем радиоавтоматики обычно задают в виде полиномов. Пусть, например, необходимо осуществить захват радиолокационной станцией движущейся цели, т.е. перейти в режим слежения (автосопровождения) по дальности и скорости (в целом и по угловым координатам). По дальности автосопровождение осуществляется системой АСД, по скорости - ЧАП или ФАП (обычно ФАП). Дальность обычно определяют, измеряя время задержки отраженного сигнала относительно излученного. Для оценки скорости измеряют доплеровский сдвиг частоты.

Для цели, движущейся с ускорением, дальность определяется известной формулой

.

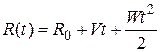Время задержки, как параметр подлежащий слежению и являющийся входным воздействием в схемной модели АСД, имеет вид полинома второго порядка

.

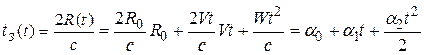Скорость цели

.

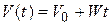Доплеровское изменение частоты, подлежащее отслеживанию, например, системой ЧАП, имеет как входное воздействие вид полинома первого порядка

.

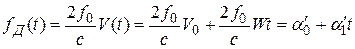Это же доплеровское изменение частоты можно отследить системой ФАП (если следить за фазой пришедшего сигнала)

.

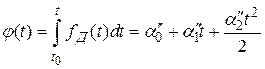Здесь фаза как входное воздействие в схемной модели системы ФАП является полиномом второго порядка.

В общем случае входной сигнал можно представить в виде полинома с конечным 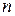или с бесконечным числом членов ряда:

.

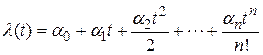Это следует из возможности разложения входного воздействия в ряд Тейлора (в окрестности точки 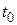по степеням )

,

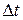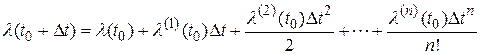или в ряд Маклорена (в окрестности точки 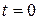по степеням )

.

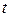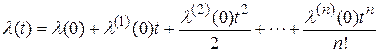Если система отрабатывает только 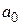с ошибкой, равной постоянной величине, то эта система имеет астатизм нулевого порядка. Если система отрабатывает 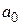и 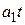с постоянной ошибкой, то эта система имеет астатизм первого порядка. Если система отрабатывает с постоянной ошибкой и слагаемое 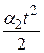, то эта система имеет астатизм второго порядка, и т.д. Для того чтобы система отработала (отследила) все слагаемые до степени 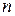включительно (включая и слагаемые с сомножителем 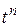) с ошибкой, равной нулю, она должна иметь порядок астатизма, равный .

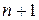Для теоретического обоснования понятия астатизма системы исследуем выражение для ошибки слежения.

Ошибка

.

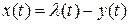В соответствии с методом импульсных характеристик

.

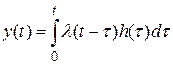Тогда

.

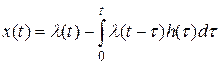Разложим 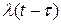в ряд Тейлора в окрестности точки 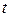по степеням :

.

Тогда

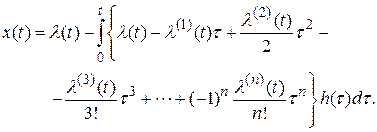
Нас будет интересовать поведение ошибки в течение некоторого достаточно большого промежутка времени для установления ее стационарного (нулевого или постоянного) значения. В этом случае можно поставить верхний предел интегрирования, равный . Тогда

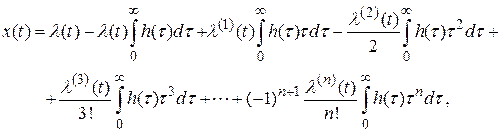
или

,

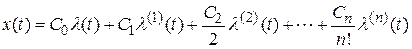где

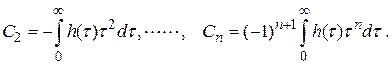
Можно предложить более простые варианты формул для расчета коэффициентов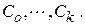

Запишем выражение для ошибки

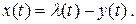
Образ ошибки по Лапласу имеет вид

.

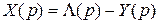Разделив это выражение на 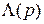, имеем

.

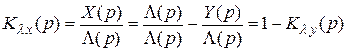Учитывая, что коэффициент передачи связан с импульсной характеристикой преобразованием Лапласа

,

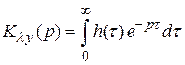получаем

.

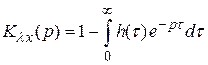Тогда нетрудно видеть, что

.

Порядком астатизма называют номер первого отличного от нуля коэффициента в этом разложении ошибки в ряд.

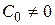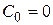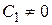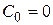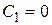Например, если , то система имеет астатизм нулевого порядка и называется астатической системой. Если , а , то система имеет астатизм первого порядка. Если и , а 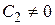, то система имеет астатизм второго порядка, и т.д. Видно, что порядок астатизма характеризует способность системы отслеживать не только саму функцию, но и ее производные.

Можно сформулировать следующее утверждение.

Если порядок воздействия как полинома, которое поступает на вход системы, меньше порядка астатизма системы, то ошибка в такой системе с течением времени стремится к нулю. Если порядок входного воздействия как полинома равен порядку астатизма системы, то ошибка в такой системе с течением времени стремится к постоянной величине. Если же порядок полинома, который действует на вход системы, выше порядка астатизма системы, то ошибка в такой системе с течением времени растет и стремится к бесконечности.

Для определения порядка астатизма необходимо рассчитать коэффициенты 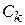по формулам (4.14), (4.15). Подсчитав число интеграторов, включенных в замкнутый контур, можно воспользоваться следующим простым правилом: Порядок астатизма равен числу этих интеграторов.

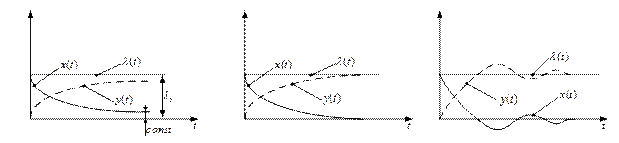
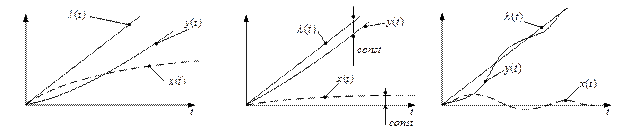
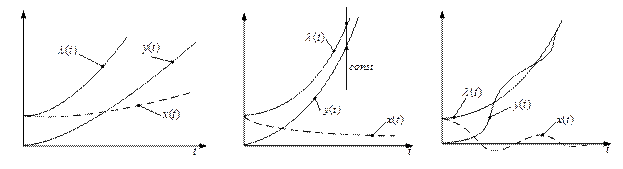
На рис. 4.9 - 4.11 показаны входные, выходные воздействия и ошибки слежения для систем с астатизмом нулевого, первого и второго порядков при воздействиях, описываемых полиномами нулевого, первого и второго порядков.

а б в

Рис. 4.9. Реакция систем с астатизмом нулевого (а), первого (б) и второго (в) порядков при входном воздействии, описываемым полиномом нулевого порядка

а б в

Рис. 4.10. Реакция систем с астатизмом нулевого (а), первого (б) и второго (в) порядков при линейном воздействии первого порядка

а б в

Рис. 4.11. Реакция систем с астатизмом первого (а), второго (б) и третьего (в) порядков при квадратичном входном воздействии

Часто для быстрого определения характера поведения динамической ошибки (выяснения лишь факта, стремится ли она к нулю или к постоянной величине) пользуются асимптотической формулой

,

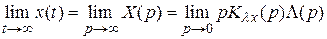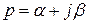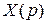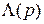где , и — преобразования Лапласа функций 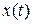, 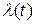; – передаточная функция системы относительно точек подачи входного воздействия 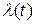и выхода контроля ошибки 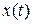, совпадающая с операторным коэффициентом передачи при замене 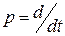на .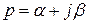

Доказательство этой формулы следует из того факта, что изображение производной функции 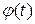имеет вид

,

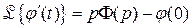т.е.

.

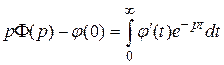Перейдя к пределу в левой и правой частях при 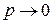, получим

,

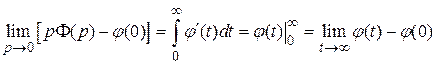откуда

.

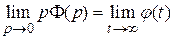Дата добавления: 2014-12-26