В качестве фильтра нижних частот

Анализ замкнутой системы с инерционным звеном

Анализ динамических систем с различными фильтрами нижних частот при регулярных воздействиях

Передаточная функция инерционного звена

.

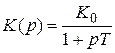Структурная схема системы (4.17) изображена на рис. 4.12. Шум .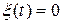

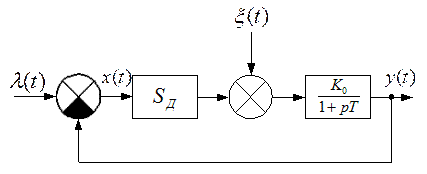
Рис. 4.12. Замкнутая система с инерционным звеном

Возможные схемы реализации передаточной функции показаны на рис. 4.13.

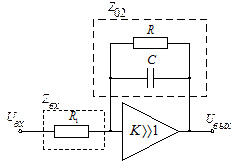
а б

Рис. 4.13. Схемы реализации инерционного звена

В схеме рис. 4.13, а 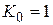и 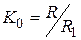. В схеме рис. 4.13, б с операционными усилителями, обладающими большим усилением (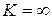), коэффициент передачи определяется как отношение .

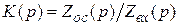Дифференциальное уравнение, связывающее динамическую ошибку с входным воздействием, определяется левым слагаемым выражения (4.5) с учетом (4.6), где :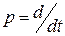

.

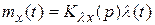Применяя преобразование Лапласа к обеим частям дифференциального уравнения (4.18), находим изображение динамической ошибки:

,

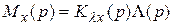где 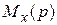— изображение ; .

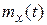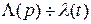Пусть входное возмущение

,

где 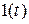— единичная функция.

Тогда с учетом выражений (4.6), (4.2) и (4.17)

.

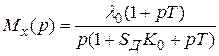Оригинал, который можно найти по таблицам,

.

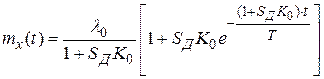График зависимостей динамической ошибки 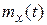и выходного процесса 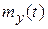показан на рис. 4.14.

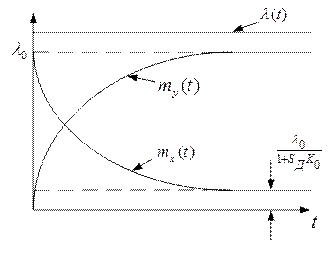
Рис. 4.14. Динамическая ошибка и выходной процесс в замкнутой системе

с инерционным звеном

Динамическая ошибка уменьшается со временем и стремится в пределе к постоянной величине 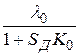. Такая система является астатической (порядок астатизма равен нулю). Астатизм системы характеризует ее способность отслеживать входное воздействие. Система, у которой порядок астатизма меньше порядка степени полинома, описывающего входное воздействие, отслеживает последнее по истечении достаточно большого промежутка времени с нулевой ошибкой. При совпадении порядка астатизма и порядка полинома ошибка отслеживания стремится к постоянной величине. Если же порядок астатизма меньше порядка степени полинома, то ошибка со временем будет увеличиваться. Обычно порядок астатизма системы равен числу интеграторов, входящих в замкнутый контур регулирования.

Скорость уменьшения ошибки (4.22) тем больше, чем меньше величина 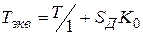, определяющая быстродействие замкнутой системы. Величину предела можно проверить по формуле (4.16):

.

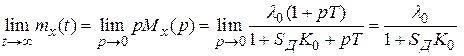Дата добавления: 2014-12-26