Властивості додавання векторів

1) властивість нульового вектора:
a+0=a;
2) асоціативність додавання:
(a+b)+c=a+(b+c);
3) комутативність додавання:
a+b=b+a;

Властивості множення вектора на число
1) комутативність:
λa=aλ;

2) асоціативність:
λ(μa)=(λμ)a;

3) дистрибутивність відносно додавання векторів:
λ(a+b)=λa+λb;
4) дистрибутивність відносно додавання чисел:
(μ+λ)a=μa+λa;

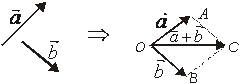
Проекцією вектора на вісь називається довжина відрізка осі , що міститься між проекціями початкової точки і кінцевої точки , взята із знаком “+”, якщо напрямок збігається з напрямком осі проекції, та із знаком “-”, якщо ці напрямки протилежні.

Легко довести основні положення теорії проекцій:

1⁰.

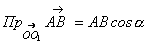
(читається: проекція на вісь дорівнює …) (рис.2.3).

2⁰.

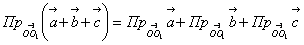
(рис.2.4).

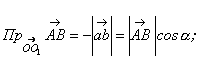
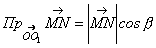
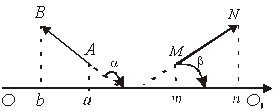
Означення. Лінійно залежними називають вектори 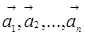, якщо існує хоч би одне дійсне число 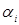(і = 1,2,…, n), що не дорівнює нулю і виконується рівність

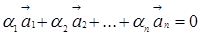(1)

Означення. Лінійно незалежними називають вектори 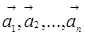, якщо рівність (7) виконується тільки тоді, коли усі .

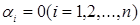В системі векторів 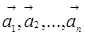число лінійно незалежних векторів дорівнює рангу матриці, яка складена з координат цих векторів.

Приклад 1. Визначити лінійну залежність або незалежність системи векторів 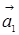= (-1,-2,-3); 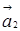= (7,8,9); 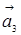= (-4,-5,6) та системи векторів 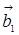= (3,-2,4,1); 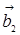= (-1,2,-1,2); 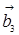= (1,2,2,5).

Розв’язування. Спочатку розглянемо систему векторів 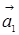, 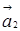та 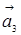. Знайдемо ранг матриці, складеної з координат цих векторів:

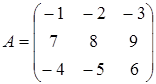
Визначник цієї матриці |А| = - 48 + 72 + 105 – 96 +84 – 45 = 72 не дорівнює нулю, тому r(A)=3 і вектори 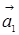, , 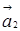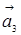лінійно незалежні.

Тепер розглянемо систему векторів 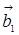, , 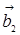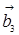. Матриця В складена з координат цих векторів має вигляд:

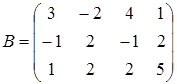
Ця матриця розміру 3 х 4 має ранг r(B)=2.

Тому вектори 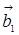, , 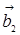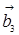лінійно залежні.

Базисом векторного простору_ називається будь-яка максимальна (повна) лінійно незалежна система векторів цього простору.

Довільний вектор 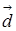n вимірного простору можна представити у вигляді лінійної комбінацій векторів базиса 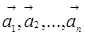так:

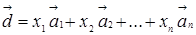(2)

Числа 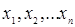називають координатами вектора 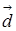у базисі векторів .

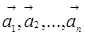6. Векторний і мішаний добуток векторів. Геометричний зміст добутків.

Векторним добутком двох векторів 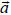та 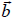, називається вектор 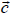, який задовольняє такі умови:

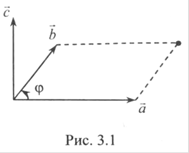
а) вектор 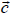перпендикулярний до площини, в якій лежать вектори 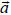та 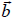(рис. 3.1);

б) вектор 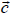напрямлений від площини, яка визначається векторами 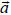та 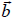, у той бік, де відбувається найкоротший поворот від вектора 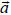до вектора 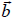проти годинникової стрілки, якщо дивитися з кінця вектора 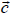, тобто вектори 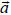, 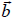і 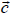утворюють праву трійку векторів;

в) довжина вектора 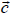чисельно дорівнює площі паралелограма, побудованого на векторах 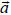та 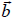як на сторонах. Векторний добуток позначають так: 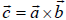або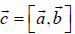



Геометричний зміст мішаного добутку:

1. 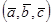- мішаний добуток векторів дорівнює орієнтованому об‘єму паралелепіпеда, побудованого на цих векторах 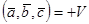, якщо трійка векторів 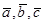- права, 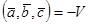, якщо трійка векторів 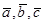- ліва, 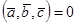, якщо трійка векторів 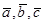- компланарні (лежать в одній площині).

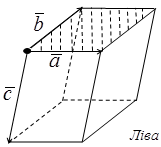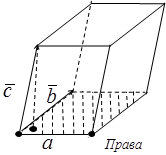2. .

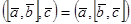3. .

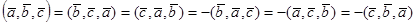Дата добавления: 2014-12-26