
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Найбільше і найменше значення функції в замкненій області
|
|
|
|
Нехай функція 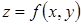 визначена і неперервна в обмеженій замкнутій області
визначена і неперервна в обмеженій замкнутій області 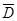 . Тоді вона досягає в деяких точках свого найбільшого
. Тоді вона досягає в деяких точках свого найбільшого  і найменшого
і найменшого 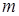 значень (т.3. глобальний екстремум). Ці значення досягаються функцією в точках, розташованих усередині області, або в точках, що лежать на межі області.
значень (т.3. глобальний екстремум). Ці значення досягаються функцією в точках, розташованих усередині області, або в точках, що лежать на межі області.
Правило знаходження найбільшого і найменшого значень диференційованої в області 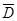 функції
функції 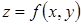 полягає в наступному:
полягає в наступному:
1. Знайти всі критичні точки функції, що належать 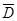 і обчислити значення функції в них;
і обчислити значення функції в них;
2. Знайти найбільше і найменше значення функції 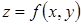 на кінцях області;
на кінцях області;
 3. Порівняти всі знайдені значення функції і вибрати з них найбільше
3. Порівняти всі знайдені значення функції і вибрати з них найбільше  і найменше
і найменше 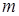 .
.
Приклад 2. Знайти щонайбільше і якнайменше значення функції 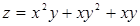 в замкнутій області, обмеженій лініями:
в замкнутій області, обмеженій лініями:
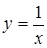 ,
, 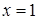 ,
, 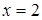 ,
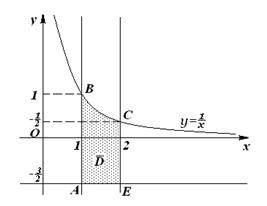
, 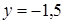 (див. рис. 7).
(див. рис. 7).
m Тут 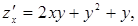
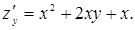
1. Знаходимо всі критичні точки:
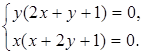
Рис. 7
Розв’язком системи є точки 
Жодна із знайдених точок не належить області 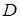 .
.
2. Досліджуємо функцію 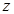 на межі області, що складається з ділянок
на межі області, що складається з ділянок  (рис. 212).
(рис. 212).
На ділянці 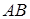 :
: 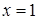 ,
, 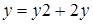 , де
, де 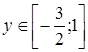
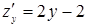 ,
, 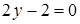 ,
, 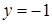 . Значення функції
. Значення функції  ,
, 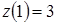 .
.
На ділянці 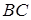 :
:
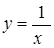 ,
, 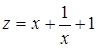 , де
, де 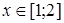 ,
,
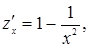
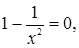
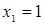 ,
, 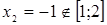 . Значення функції
. Значення функції 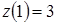 ,
, 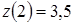 .
.
На ділянці 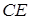 :
: 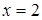 ,
, 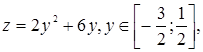
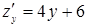 ;
; 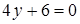 ;
;  . Значення функції
. Значення функції 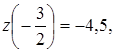
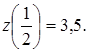
На ділянці 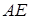 :
: 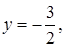
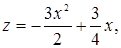
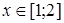 ,
,
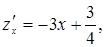
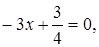
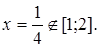 Значення функції
Значення функції 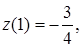
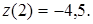
3. Порівнюючи отримані результати, маємо:  а
а
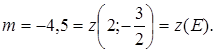
54. Поняття невизначеного інтеграла. Його геометричний зміст.
Множина всіх первісних функцій 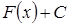 для
для  називається невизначеним інтегралом від функції
називається невизначеним інтегралом від функції  і позначається символом
і позначається символом 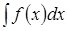 .
.
Таким чином, за означенням
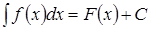 .
.
Тут  називається підінтегральною функцією,
називається підінтегральною функцією, 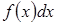 – підінтегральним виразом,
– підінтегральним виразом, 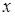 – змінною інтеграції,
– змінною інтеграції, 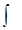 – знак невизначеного інтеграла.
– знак невизначеного інтеграла.
Операція знаходження невизначеного інтеграла від функції називається інтегруванням цієї функції.
Геометрично невизначений інтеграл є сімейством «паралельних кривих» 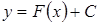 (кожному числовому значенню
(кожному числовому значенню 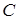 відповідає певна крива сімейства) (див. рис. 166). Графік кожної первісної (кривої) називається інтегральною кривою.
відповідає певна крива сімейства) (див. рис. 166). Графік кожної первісної (кривої) називається інтегральною кривою.
Чи для всякої функції існує невизначений інтеграл?
Має місце теорема, що стверджує, що «будь-яка неперервна на 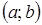 функція має на цьому проміжку первісну», а отже, і невизначений інтеграл.
функція має на цьому проміжку первісну», а отже, і невизначений інтеграл.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 16752; Нарушение авторских прав?; Мы поможем в написании вашей работы!