Похідна складної функції кількох змінних

Диференціали вищих порядків.

Повний диференціал функції (формула (2.5)) називають також диференціалом першого порядку.

Нехай функція 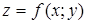має неперервні частинні похідні другого порядку. Диференціал другого порядку визначається по формулі 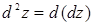. Знайдемо його:

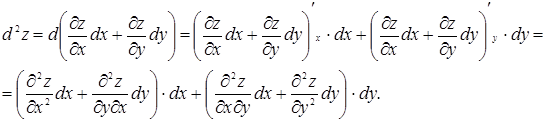
Звідси:

Символічно це записується так: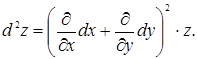

Аналогічно можна отримати формулу для диференціала третього порядку:

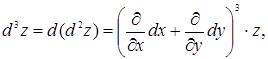
де

Методом математичної індукції можна показати, що

Відзначимо, що отримані формули справедливі лише у разі, коли змінні 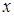і 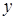функції 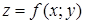є незалежними.

Приклад 4. (Для самостійної роботи) Знайти , якщо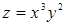

Відповідь: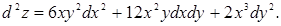

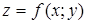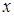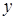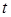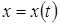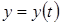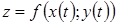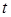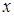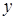Нехай - функція двох змінних і , кожна з яких є функцією незалежної змінної : , . В цьому випадку функція є складною функцією однієї незалежної змінної ; змінні і – проміжні змінні.

Теорема 10.2.4. Якщо 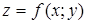- диференційовна в точці 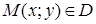функція і

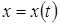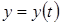і - функції незалежної змінної 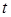, також диференційовні, то похідна складної функції 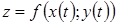обчислюється по формулі

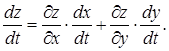(2.8)

Окремий випадок: 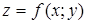, де 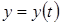, тобто - складна функція однієї незалежної змінної 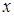. Цей випадок зводиться до попереднього, причому роль змінної 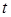грає 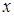. Згідно формули (2.8) маємо:

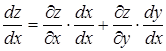або

Формула (2.9) носить назву формули повної похідної.

Загальний випадок: 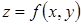, де , 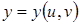. Тоді 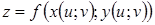– складна функція незалежних змінних 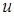і .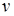

Її частинні похідн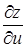і і 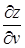можна знайти, використовуючи формулу (2.8). Таким чином, зафіксувавши 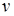, замінюємо в ній 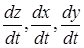відповідними частинними похідними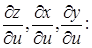

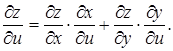
Аналогічно одержуємо: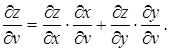

Таким чином, похідна складної функції 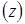по кожній незалежній змінній ( 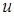і 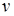) рівна сумі частинних похідних цієї функції 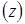по її проміжних змінних ( 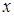і 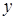) на їх похідні по відповідній незалежній змінн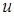і ( і ).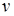

Приклад 5. Знайти 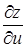і 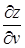, якщо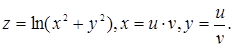

m Знайдемо 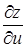( 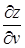– самостійно), використовуючи формулу (2.10):

Спростимо праву частину отриманої рівності:

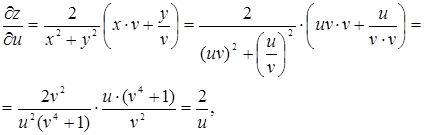
тобто

Дата добавления: 2014-12-26