Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

Практическое занятие № 40

Тема занятия « Знакоположительные ряды. Знакочередующиеся ряды, признак Лейбница »

Цель занятия: формирование умений и навыков исследовать знакоположительные и знакочередующиеся ряды.

Организационная форма занятия: практикум с применением интерактивной доски.

Компетенции, формируемые на занятии:

способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1).

Формирование у будущих специалистов этой компетенций на занятии предполагает обучение студентов

- сформулировать гипотезу и проверить ее в дальнейшем;

- анализировать ситуации и делать выводы;

- ставить новые вопросы и видеть проблемы в традиционных ситуациях;

- абстрагировать содержание и выделять существенное;

- применение численных методов решения базовых математических задач в практической деятельности.

1. Радикальный признак Коши.

2. Интегральный признак Коши.

3. Нахождение суммы числового ряда.

4. Знакочередующиеся ряды, признак Лейбница.

Для подготовки к занятию дома

i. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

ii. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

iii. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

iv. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

v. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

3. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия.

Дома

1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

2. Подготовьтесь к самостоятельной работе №13 по теме «Числовые ряды». Примерный вариант работы вы можете найти в программе дисциплины.

Рекомендуемая литература

[1] глава 10 пп 10.1.

[2] часть 2, глава III §1.

[3] глава 5 §§ 21– 22.

[6] глава 14 § 3.

[7] глава XIV § 3.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. Исследуйте ряд на сходимость.

Решение. Воспользуемся радикальным признаком Коши: . Так как , то ряд сходится.

2. Проверьте, сходится ли ряд ?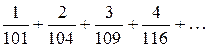

Решение. Запишем общий член ряда . Введем в рассмотрение функцию 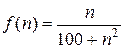. Эта функция непрерывная и невозрастающая при 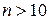, так как при

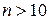. Воспользуемся интегральным признаком Коши:

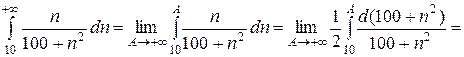
, следовательно данный ряд расходится.

3. Найдите сумму ряда .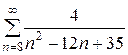

Решение. Разложим дробь 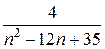на элементарные с помощью метода неопределенных коэффициентов:

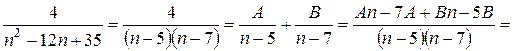
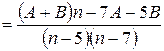, отсюда , , .

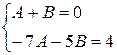Следовательно, .

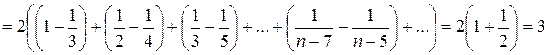4. Проверьте сходимость ряда .

Решение. Ряд сходится, так как удовлетворяет условиям признака Лейбница:

1) 2)

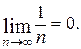
Данный ряд сходится условно, так как ряд, составленный из его абсолютных величин - гармонический ряд, расходится.

5. Исследуйте сходимость ряда .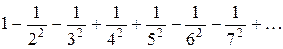

Решение. Ряд 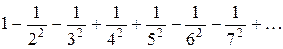является знакопеременным. Этот ряд является абсолютно сходящийся, так как сходится ряд, составленный из абсолютных величин членов данного ряда: (в этом легко убедиться с помощью интегрального признака Коши).

Теоретические задания

Дата добавления: 2014-12-26