Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

Практическое занятие № 41

Тема занятия « Степенные ряды и область их сходимости. Разложение функций в степенной ряд »

Цель занятия: Сформировать умения и навыки разложения функций в степенной ряд и находить область сходимости степенного ряда.

Организационная форма занятия: практикум с применением интерактивной доски.

Компетенции, формируемые на занятии:

способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1).

Формирование у будущих специалистов этой компетенций на занятии предполагает обучение студентов

- разлагать основные элементарные функции в ряд и исследовать ряд на сходимость, применять полученные навыки в других областях математического знания и дисциплинах естественнонаучного содержания;

- сформулировать гипотезу и проверить ее в дальнейшем;

- анализировать ситуации и делать выводы;

- абстрагировать содержание и выделять существенное.

1. Степенные ряды и область их сходимости.

2. Разложение функций в степенной ряд.

3. Определение области сходимости степенного ряда.

4. Почленное дифференцирование и интегрирование степенных рядов.

Для подготовки к занятию дома

1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

6. Подготовьтесь к самостоятельной работе №13 по теме «Числовые ряды». Примерный вариант работы вы можете найти в программе дисциплины.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

3. Решите предложенный преподавателем вариант самостоятельной работе №13 по теме «Числовые ряды» и сдайте выполненную работу на проверку преподавателю.

4. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия.

Дома

1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

2. Приступите к выполнению ИДЗ № 9 по теме «Ряды» в соответствии с Вашим вариантом. Рекомендуется выполнить первое задание ИДЗ. Текст ИДЗ приведен в конце разработки этого занятия.

Рекомендуемая литература

[1] глава 10 пп 10.2.

[2] часть 2, глава III §§ 3-4.

[3] глава 5 § 23.

[6] глава 14 § 5.

[7] глава XIV § 5.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. Найдите радиус и интервал сходимости степенного ряда

.

Решение. Это степенной ряд, все коэффициенты его, за исключением , отличны от нуля. Найдем радиус и интервал сходимости данного ряда. Здесь и . Поэтому

.

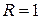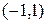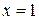Следовательно, радиус сходимости и ряд сходится на интервале . Исследуем поведение ряда на концах интервала сходимости, т.е. в точках . При получаем гармонический ряд 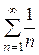, а при 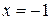- ряд , который сходится в силу признака Лейбница. Таким образом, данный ряд сходится в любой точке полуинтервала и расходится вне его.

2. Определить область сходимости степенного ряда .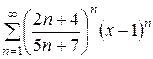

Решение. Воспользуемся формулой Коши – Адамара:

. Тогда интервал сходимости 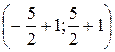, то есть . В точках и исследуем отдельно.

При имеем знакочередующийся ряд .

При 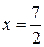имеем знакоположительный ряд .

Применим необходимый признак сходимости рядов:

,

так как , , 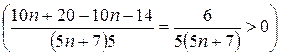следовательно при и 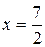ряд расходится. Таким образом, - интервал сходимости данного ряда.

3. Определите интервал сходимости ряда .

Решение. Для нахождения интервала сходимости ряда воспользуемся радикальным признаком Коши:

,

отсюда 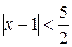, , 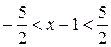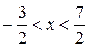- интервал сходимости данного ряда.

4. Определите интервал сходимости ряда .

Решение. Воспользуемся признаком Даламбера. Выпишем 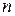-й и 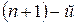члены ряда: , . Тогда находим

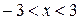- интервал сходимости ряда.

При 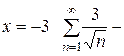ряд с положительным членами. Так как для любого натурального 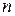(, , 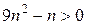), следовательно, ряд расходится.

При 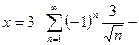ряд сходится, но условно.

Заметим, что так как среди коэффициентов данного ряда - нет равных нулю, то для нахождения радиуса сходимости можно было воспользоваться формулой 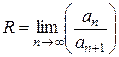. Тогда вычисляем

.

Следовательно 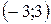- интервал сходимости.

5. Разложите в ряд Маклорена функцию .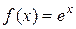

Решение. Если функция 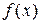на интервале 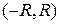разлагается в степенной ряд 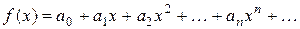, то коэффициенты этого ряда определяются по формулам

, .

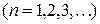Подставляя выражения коэффициентов, получаем ряд

, (*)

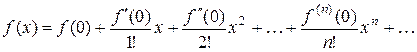который называется рядом Маклорена для функции .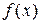

Имеем откуда при 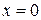получаем . Подставляя полученные числа в формулу (*), находим

Так как , то ряд сходится на всей числовой прямой.

6. Разложите в ряд Маклорена функцию .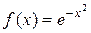

Решение. Воспользуемся разложением функции , полученным выше. Положим тогда . Имеем

.

При находим искомое разложение

,

которое справедливо, очевидно, для всех значений x.

7. Разложите в ряд Маклорена функцию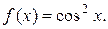

Решение. Имеем 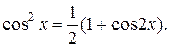Используя формулу 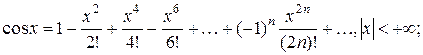, запишем разложение функции заменив там на :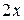

,

или

.

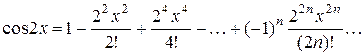Таким образом,

.

Окончательно получаем

.

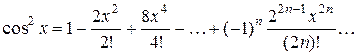Полученный ряд сходится при всех .

8. Разложите в ряд Маклорена функцию .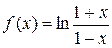

Решение. Имеем Воспользовавшись известным разложением ,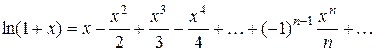

можем записать

.

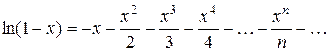Отсюда получаем

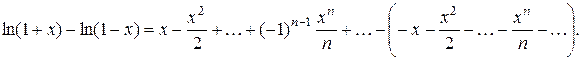
Раскрывая скобки и приводя подобные члены, находим искомое разложение:

.

Очевидно, ряд сходится в интервале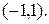

9. Разложить в ряд Маклорена функцию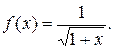

Решение. Имеем Воспользовавшись разложением

,

нетрудно получить разложение

,

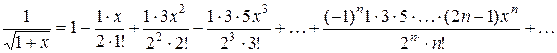справедливое для интервала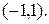

10. Найдите сумму ряда .

Решение. Рассмотрим ряд , исследуем его на сходимость:

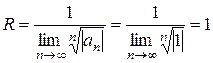, при 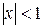- ряд сходится (при - расходится). Сумма этого ряда , так как ряд представляет собой геометрическую прогрессию. Таким образом, . Проинтегрируем обе части полученного разложения:

,

,

.

11. Найдите сумму ряда .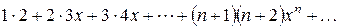

Решение. Воспользуемся бесконечной геометрической прогрессией

(сходится при ).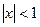

Дважды продифференцируем ряд:

,

.

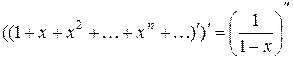Теоретические задания

Дата добавления: 2014-12-26