Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

Практическое занятие № 44

Тема занятия « Функции нескольких переменных. Частные производные функции нескольких переменных »

Цель занятия: изучить определения частных производных и правила их нахождения.

Организационная форма занятия: практикум.

Компетенции, формируемые на занятии:

- способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1).

Формирование у будущих специалистов этой компетенции на занятии предполагает обучение студентов

- сформулировать гипотезу и проверить ее в дальнейшем;

- анализировать ситуации и делать выводы;

- ставить новые вопросы и видеть проблемы в традиционных ситуациях;

- абстрагировать содержание и выделять существенное.

1. Функции нескольких переменных, основные определения.

2. Частные производные первого порядка.

3. Частные производные второго и более высоких порядков.

4. Теорема о независимости смешанных производных от порядка дифференцирования.

5. Производная сложной функции. Полная производная.

Для подготовки к занятию дома

i. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

ii. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

iii. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

iv. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

v. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

3. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия.

4. Сдайте выполненное ИДЗ №9 на проверку преподавателю.

Дома

1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

2. Пройдите репетиционное тестирование по пройденной теме.

Рекомендуемая литература

[1] глава 11 пп 11.1 - 11.3.

[2] часть 1, глава VIII §§ 1 – 2.

[3] глава 6 §§ 27, 30.

[4] часть II занятия 37 – 39.

[6] глава 12 § 1; § 6.

[7] глава VIII §§1; 2; 6.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. Укажите область определения функции .

Решение. Аналитическое выражение 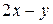имеет смысл при любых значениях и 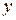. Следовательно, областью определения функций является вся плоскость

2. Найдите область определения функции

Решение. Для того чтобы 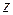имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. и 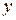должны удовлетворять неравенству 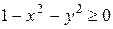, или .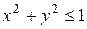

Все точки ,координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 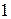с центром в начале координат и на границе этого круга.

3. Найдите частные производные первого порядка для функции .

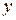Решение. Вычисляем частную производную функции по переменной при этом считаем, что - постоянная величина:

.

Аналогично, считая, что - постоянная вычисляем частную производную по переменной :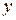

.

4. Вычислите частные производные второго порядка для функции .

Решение. Воспользуемся найденными частными производными первого порядка и 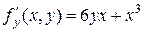, которые сами являются функциями двух переменных и 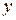. Далее дифференцируем каждую из частных производных первого порядка по каждой из двух переменных. В результате получаем четыре частные производные второго порядка:

;

;

;

.

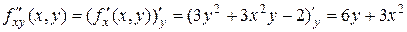Заметим, что смешанные частные производные равны, т.е. .

5. Для сложной функции вычислите частные производные первого порядка.

Решение. Для нахождения частных производных для сложной формулы воспользуемся формулами 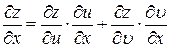и . Вычисляем частные производные входящие , , , , , .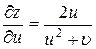

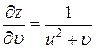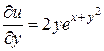Тогда получаем

,

.

В последние выражения вместо 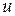и 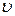необходимо поставить и соответственно.

Замечание. Для случая большего числа переменных формулы нахождения частных производных обобщаются. Например, если - функция четырех аргументов 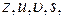а каждый из них зависит от и 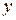, то указанные формулы принимают вид

,

.

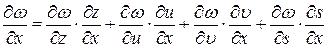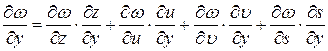Если задана функция , где в свою очередь зависят от одного аргумента : то, 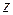является функцией только одного переменного и можно ставить вопрос о нахождений производной 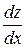. Эта производная вычисляется по первой из приведенных формул: . Но так как - функция только одного , то частные производные обращаются в обыкновенные; кроме того, ; поэтому . Эта формула носит название формулы для вычисления полной производной 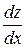(в отличие от частной производной ).

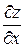6. Вычислите полную производную функции 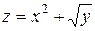, если .

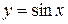Решение. Воспользуемся формулой вычисления полной производной 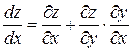. Вычисляем , , 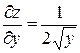. Тогда подставляя в формулу, получаем следующий результат:

.

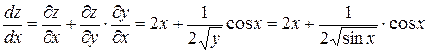Теоретические задания

Дата добавления: 2014-12-26