
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные определения кинематики
|
|
|
|
1. Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени.
2. Материальная точка (МТ) – тело, размерами которого можно пренебречь при описании его движения.
3. Траектория – линия в пространстве, вдоль которой движется МТ (совокупность последовательных положений МТ, занимаемых ею в процессе движения).
4. Система отсчета (СО) включает в себя:
· тело отсчета;
· систему координат, связанную с этим телом;
· прибор для измерения времени, включая выбор начальной точки отсчета времени (при этом, если используются несколько часов, то они должны быть синхронизированы).
5. Основная (обратная) задача кинематики: найти закон (уравнения) движения тела в заданной системе отсчета.
Например, уравнения движения тела, брошенного под углом к горизонту, выглядят так:
 ,
, 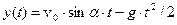 .
.
При этом все остальные задачи, нахождение пути, высоты подъема, дальности, времени являются вспомогательными и, как правило, легко решаются на основании уравнений движения. Прямая задача кинематики заключается в вычислении параметров движения по заданным уравнениям движения.
6. Поступательное движение однозначно определяется по одному из следующих признаков:
· все точки тела движутся по траекториям одинакового вида;
· любой отрезок прямой линии, проведенный внутри тела, при поступательном движении остается параллельным самому себе;
· все точки тела движутся с одинаковой скоростью.
7. Вращательное движение – такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения
Плоское движение твердого тела можно разложить на поступательное и вращательное движение.
8. Путь – это длина траектории (измеренная с учетом кратности прохождения отдельных ее участков).
9. Средняя скорость – это векторная физическая величина, равная отношению перемещения к промежутку времени, за который это перемещение осуществлено.
10. Среднее значение модуля скорости (средняя путевая скорость) – это скалярная физическая величина, равная отношению пути к промежутку времени, за который пройден этот путь.
11. Мгновенная скорость -это векторная физическая величина, равная первой производной вектора перемещения (или радиус-вектора) по времени:  ,
,
или 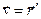 , в проекциях получаем:
, в проекциях получаем:  и т.д.
и т.д.
12. Ускорение- -это векторная физическая величина, равная первой производной вектора скорости по времени:
 , в проекциях получаем:
, в проекциях получаем: 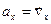 и т.д.
и т.д.
Таблица типов движения:
Таблица 6
Равномерное движение: 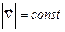
| Равнопеременное движение: 
| ||
Прямолинейное равномерное

| Криволинейное равномерное | Равноускоренное 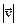 увеличивается увеличивается
| Равнозамедленное 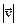 уменьшается уменьшается
|
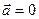
| 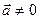
| 
| 
|
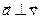
|
13. Уравнение (закон) равнопеременного движения:
 , или в координатной форме:
, или в координатной форме:  .
.
14. Уравнение (закон) изменения скорости при равнопеременном движении: 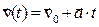 , или в координатной форме:
, или в координатной форме: 
15. Формула для средней скорости при равнопеременном движении :
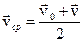 .
.
16.
|
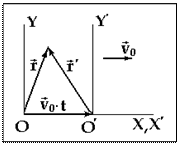 Преобразования Галилея, формула сложения скоростей:
Преобразования Галилея, формула сложения скоростей:Пусть имеются две системы отсчета, К и К’, причем К’ движется вдоль положительного направления X с постоянной скоростью
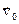 и в начальный момент времени начала координат совпадали, тогда очевидно
и в начальный момент времени начала координат совпадали, тогда очевидно 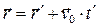 ,
,  - это и есть преобразования координат, времени Галилея. Продифференцировав преобразования Галилея по времени, получим классическую формулу сложения скоростей
- это и есть преобразования координат, времени Галилея. Продифференцировав преобразования Галилея по времени, получим классическую формулу сложения скоростей 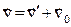 .
.Скорость МТ относительно условно неподвижной системы отсчета равна векторной сумме скоростей, относительно подвижной СО и подвижной СО относительно неподвижной.
17. Формула для пути с исключенным временем:  .
.
Основные определения кинематики вращательного движения:
18. Период – это значение интервала времени, за который тело совершает полный оборот по циклической траектории.
Частота – величина обратная периоду,  ,
,  .
.
Число оборотов в секунду равно частоте, но обозначается n,  .
.
19. Угловая скорость – скалярная величина, равная первой производной угла поворота по времени,  . Далее мы введем угол и угловую скорость как векторные величины. При равномерном движении
. Далее мы введем угол и угловую скорость как векторные величины. При равномерном движении  .
.
20. Ускорение при криволинейном движении – имеет две составляющие: тангенциальную, отвечающую за изменение скорости по величине и нормальную, или центростремительную, отвечающую за искривление траектории
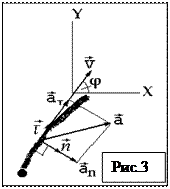
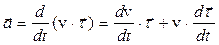
С учетом выражения 

окончательно получаем: 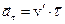 ,
, 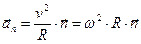 , где
, где  -единичный вектор, направленный к центру кривизны,
-единичный вектор, направленный к центру кривизны,  - единичный вектор вдоль касательной к траектории. Более компактный вывод выглядит так:
- единичный вектор вдоль касательной к траектории. Более компактный вывод выглядит так:  , следовательно,
, следовательно, 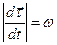 и
и  .
.
Типичные  задачи кинематики:
задачи кинематики:
Задача №2. Чему равна скорость точек A,B,C,D на диске, рис.4, катящемся по плоскости без проскальзывания (чистое качение).
Изобразите геометрическое место точек диска, у которых скорость по модулю равна скорости поступательного движения диска.
Задача № 3. Два автомобиля едут в попутном направлении с заданной скоростью.На какой минимальной дистанции необходимо держаться второму автомобилю, чтобы обезопасить себя от попадания камней, вырывающихся из-под колес первого автомобиля. Под каким углом к горизонту в системе отсчета, связанной с землей вылетают самые опасные камни? Сопротивлением воздуха пренебречь.
Ответ: 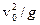 ,
,  - вперед по ходу движения.
- вперед по ходу движения.
Задача № 4. Критическое для тела человека кратковременное ускорение (при котором есть шанс избежать серьезных травм) равно  . Каким должен быть минимальный тормозной путь, если начальная скорость автомобиля равнялась 100км/ч?
. Каким должен быть минимальный тормозной путь, если начальная скорость автомобиля равнялась 100км/ч?
Задача № 5. (№1.23 из сборника задач [5]).Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости 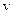 по закону
по закону 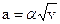 , где
, где 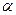 - положительная постоянная. В начальный момент скорость точки равна
- положительная постоянная. В начальный момент скорость точки равна  . Какой путь она пройдет до остановки? За какое время этот путь будет пройден?
. Какой путь она пройдет до остановки? За какое время этот путь будет пройден?
Решение: записывая выражение для модуля ускорения  и, разделяя переменные, получим:
и, разделяя переменные, получим:  . Интегрируя с учетом начального условия
. Интегрируя с учетом начального условия 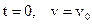 , получим:
, получим:  .
.
Остановке соответствует момент времени 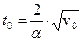 .
.
Интегрируя выражение для скорости, получаем 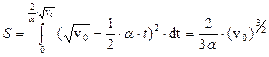 . Ответ:
. Ответ: 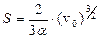 .
.
Задача №6 (№ 1.39 из сборника задач [5]). Точка движется по дуге окружности радиуса R. Ее скорость зависит от пройденного пути S по закону 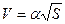 , где
, где 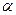 – постоянная. Найти угол
– постоянная. Найти угол 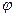 между вектором полного ускорения и вектором скорости в зависимости от S.
между вектором полного ускорения и вектором скорости в зависимости от S.
Решение: 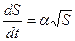 . Разделив переменные и проинтегрировав, получим:
. Разделив переменные и проинтегрировав, получим:  ;
;  ;
;  ;
; 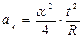 ;
; 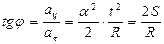 .
.
Вопросы для контроля:
Ø Можно ли утверждать, что каждая частица покоится в собственной системе отсчета?
Ø Можно ли утверждать, что ускорение автомобиля равно нулю, если спидометр все время показывает одно и тоже значение?
Ø В какой точке траектории снаряд имеет наименьшую скорость?
Ø В чем ошибочность утверждения, что равнопеременное движение – это движение с постоянным по величине ускорением?
Ø Как вы себе представляете синхронизацию часов, находящихся в разных частях пространства?
Ø Можно ли по уравнению траектории восстановить уравнение движения тела?
Ø Могут ли вектора скорости и ускорения составлять между собой тупой угол?
Ø Как связаны между собой линейная и угловая скорость?
Тангенциальное и угловое ускорения?
Ø В каких системах отсчета выполняется классическое правило сложения скоростей?
Ø В чем суть преобразований Галилея?
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1701; Нарушение авторских прав?; Мы поможем в написании вашей работы!