
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Назначение критерия
|
|
|
|
Параметрический критерий Стьюдента
Критерий Стьюдента применяется:
А) для сравнения любых двух параметров распределений или проверки гипотез о случайности различий между параметрами (Н0);
Б) для интервального оценивания (является ли параметр, полученный на выборочной совокупности, параметром генеральной совокупности);
В) для оценки статистической значимости мер связи (коэффициентов корреляции).
Ограничения в использовании критерия:
1. Критерий Стьюдента применяется для сравнения параметров признаков, измеренным по интервальной или пропорциональной шкалам.
2. Распределение признака должно быть нормальным.
3. Ограничений по объему выборки нет
Алгоритм расчета критерия для независимых выборок:
1. Для каждой выборки отдельно рассчитываются параметры распределений. Таким образом, мы имеем:
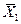 — среднее арифметическое значение признака в выборке 1;
— среднее арифметическое значение признака в выборке 1;
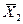 — среднее арифметическое значение признака в выборке 2;
— среднее арифметическое значение признака в выборке 2;
σ1 — стандартное отклонение признака в выборке 1;
σ2 — стандартное отклонение признака в выборке 2;
N1 — объем (количество испытуемых) выборки 1;
N2 — объем (количество испытуемых) выборки 2.
А) Выборки разного объема N1≠ N2
2) Вычисляется величина, характеризующая различия изменчивости результатов в двух выборках:
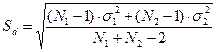
3) Находим расчетное (эмпирическое) значение критерия Стьюдента по следующей формуле:
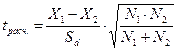
4) Для того, чтобы найти по таблице критических значений табличное значение критерия, находим число степеней свободы по формуле:
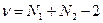
Б) Выборки одинакового объема N1= N2 = N (после расчета параметров распределений можно сразу вычислить расчетное значение критерия)
2) Находим расчетное (эмпирическое) значение критерия Стьюдента по следующей формуле:
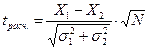
3) Для того, чтобы найти по таблице критических значений табличное значение критерия, находим число степеней свободы по формуле:
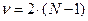
Алгоритм расчета критерия Стьюдента для зависимых выборок:
1) Для удобства расчетов целесообразно составить таблицу следующего вида:
Таблица 15
| № | X 1i | X 2i | d i | d i- 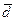
| (d i- 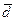 )2 )2
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| ….. | |||||
| N | |||||
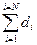
| 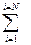 (d i- (d i- 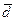 )2 )2
|
В этой таблице:
столбик 1 — номера испытуемых по порядку в списке;
столбик 2 — X 1i — значения признака в данной выборке в ситуации 1;
столбик 3 — X 2i — значения признака в данной выборке в ситуации 2.
2) Для каждой пары измерений в двух ситуациях находим их разницу (сдвиг значений) — столбик 4:
d i = X 2i – X 1i
3) Для выборки значений d i определяем параметры: средний арифметический сдвиг и стандартное отклонение сдвига.
Для среднего арифметического необходимо найти сумму всех сдвигов (по столбику 4) и подставить в формулу:
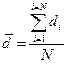
Для вычисления стандартного отклонения необходимо:
а) найти разность каждого значения сдвига и среднего арифметического сдвига — столбик 5;
б) возвести каждую разность в квадрат — столбик 6;
в) найти сумму квадратов разностей (по столбику 6) и подставить найденную сумму в формулу:
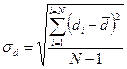
4) Вычисляем расчетное значение критерия Стьюдента по формуле:
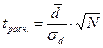
5) Находим число степеней свободы:
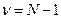
Правило вывода (правило принятия решения)
Критические (табличные) значения критерия Стьюдента находятся по таблице критических значений для этого критерия (см. приложение 1.2) в зависимости от числа степеней свободы (формулы для их вычисления приведены выше).
Если 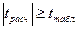 , то Н0 отвергается, то есть сравниваемые параметры (средние арифметические, полученные в двух ситуациях) статистически различаются.
, то Н0 отвергается, то есть сравниваемые параметры (средние арифметические, полученные в двух ситуациях) статистически различаются.
Если  <
< 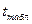 , то Н0 принимается, то есть сравниваемые параметры (средние арифметические, полученные в двух ситуациях) статистически не различаются.
, то Н0 принимается, то есть сравниваемые параметры (средние арифметические, полученные в двух ситуациях) статистически не различаются.
Возможны случаи, когда значимость различий между средними обусловлена не различием средних арифметических генеральных совокупностей, а различием их дисперсий. Результат сравнения средних в этом случае будет искажен. Поэтому при использовании критерия Стьюдента для сравнения средних арифметических рекомендуется всегда оценивать и расхождение между дисперсиями.
Сравнить дисперсии можно двумя способами:
А) для нормальных распределений большого объема можно использовать критерий Стьюдента и оценить различия между стандартными отклонениями.
 ,
,
где σ1 и σ2 — стандартные отклонения 1-й и 2-й выборок;
N1 и N2 — число испытуемых в 1-й и 2-й выборках.
Правило принятия решения:
Если 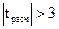 , то различия между дисперсиями статистически значимы. Если
, то различия между дисперсиями статистически значимы. Если 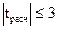 , то дисперсии статистически не различаются.
, то дисперсии статистически не различаются.
Б) Для малочисленных выборок из нормально распределенной генеральной совокупности используется
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 988; Нарушение авторских прав?; Мы поможем в написании вашей работы!