Алгоритм расчета критерия Розенбаума

Ограничения критерия

Назначение критерия

Непараметрические критерии для сравнения независимых выборок

Непараметрический критерий Розенбаума (критерий «хвостов»)

Критерий Розенбаума применяется для оценки различий между двумя выборками по уровню какого-либо признака.

Этот метод сравнивает два ряда упорядоченных значений и определяет, достаточно ли сильно они различаются или насколько велика область значений в выборках, которые не пересекаются. При этом 1-м рядом (выборкой, группой) называется тот ряд значений, в котором значения, по предварительной оценке, выше, а 2-м рядом — тот, где они предположительно ниже.

Чем больше область неперекрещивающихся значений (чем больше «хвосты»), тем более вероятно, что различия достоверны.

Расчетное (эмпирическое) значение критерия Q отражает то, насколько велика зона совпадения между рядами. Поэтому чем больше Q_эмп., тем более вероятно, что различия достоверны.

1. Признак должен быть измерен по ординальной, интервальной или пропорциональной шкале.

2. Выборки должны быть независимыми.

3. В каждой выборке должно быть не меньше 11 наблюдений. Объемы выборок должны примерно совпадать. При этом указываются следующие правила:

а) если в каждой выборке меньше 50 наблюдений, то абсолютная величина разности между N₁ и N₂ должна быть больше 10 наблюдений;

б) если в каждой выборке больше 51 наблюдения, но меньше 100, то абсолютная величина разности между N₁ и N₂ не должна быть больше 20 наблюдений;

в) если в каждой выборке больше 100 наблюдений, то допускается, чтобы одна из выборок была больше другой не более чем в 1,5-2 раза.

3. Диапазоны разброса значений (x_max–x_min) в двух выборках не должны совпадать между собой. Применение критерия бессмысленно, если «хвосты» равны 0. Однако при этом между средними могут существовать статистически значимые различия, обусловленные, например, разносторонне направленной асимметрией распределений.

1. В каждой выборке отдельно упорядочить значения признака по возрастанию. При этом считать 1-й выборку тот ряд значений, в котором значения по предварительной оценке выше, а 2-й — ту выборку, в которой значения предположительно ниже.

2. Найти самое высокое значение в выборке 2.

3. Подсчитать количество значений в выборке 1, которые выше максимального значения в выборке 2. Обозначить эту величину как S₁.

4. Найти в выборке 1 самое маленькое значение.

5. Подсчитать количество значений в выборке 2, которые ниже минимального значения в выборке 1. Обозначить эту величину как S₂.

6. Вычислить расчетное значение критерия Розенбаума по формуле Q_эмп.=S₁+S₂

Эти шаги проиллюстрированы на рисунке 17.

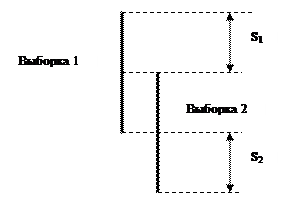
Рис. 17. Критерий Розенбаума

7. Правило принятия решения (правило вывода):

Если N₁,N₂<26, то по таблице критических значений критерия Розенбаума (см. соответствующее приложение в книге Сидоренко Е. В.) в зависимости от N₁ и N₂ найти критическое значение критерия.

Если N₁,N₂>26, то Q_эмп.=8 при р =0,95 и Q_эмп.=10 при р=0,99.

Если Q_эмп. < Q_кр. , различия между выборками статистически незначимы, Н₀ принимается, то есть статистически значимых различий по выраженности признака в двух независимых выборках нет.

Если Q_эмп. ≥ Q_кр. , различия между выборками статистически достоверны, Н₀ отвергается и принимается Н₁, то есть в одной из выборок статистически значимо чаще встречаются более высокие значения.

Дата добавления: 2014-12-26