Поправка Снедекора

Статистически значимое различие дисперсий указывает на то, что генеральные совокупности, из которых взяты выборки, также имеют разные дисперсии. В этом случае рекомендуется при сравнении средних арифметических значений с помощью критерия Стьюдента вводить в критерий поправку по Снедекору.

Назначение критерия

Параметрическийкритерий Фишера.

Критерий Фишера применяется:

а) для сравнения двух дисперсий;

б) для проверки гипотезы о значимости коэффициентов детерминации;

в) для проверки гипотезы об однородности ряда средних арифметических значений.

Ограничения в использовании критерия: критерий применяется для сравнения признаков, измеренных в интервальной или пропорциональной шкале.

Критерий Фишера рассчитывается по следующей формуле:

,

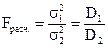где σ₁ и σ₂ — стандартные отклонения 1-й и 2-й выборок;

D₁ и D₂ — дисперсии в 1-й и 2-й выборках.

В формуле критерия Фишера в числитель дроби всегда ставится большая величина, то есть σ₁ > σ₂ или D₁ > D₂.

Правило принятия решения:

Расчетное значение критерия Фишера необходимо сравнить с критическим (табличным) значением (см. таблицу критических значений критерия Фишера — приложение 1.3), которое находится в зависимости от двух значений — числа степеней свободы для каждой выборки. Число степеней свободы находится по следующим формулам:

ν₁ = N₁ – 1 и ν₂ = N₂ – 1

Если F_расч. > F_{критич.}, то различия между дисперсиями статистически значимы. Если F_расч. ≤ F_{критич.}, то дисперсии статистически не различаются.

Критерий Стьюдента рассчитывается обычным способом. Поправка Снедекора заключается в том, что расчетное значение сравнивают не с обычным критическим значением, а с иным, которое повышает это критическое значение.

Если сравниваются выборки равного объема, то есть N₁= N₂=N, то табличное значение находят для числа степеней свободы, вычисленное по формуле: ν = N – 1.

Если сравниваются выборки разного объема, то вычисляют среде взвешенное табличное значение критерия Стьюдента следующим образом.

Для каждой из выборок находят свое число степеней свободы по формулам: ν₁ = N₁ – 1 и ν₂ = N₂ – 1.

В зависимости от ν₁ по таблице критических значений (приложение 1.2) находят t_{табл. 1} и в зависимости от ν₂ находят t_{табл. 2}.

Далее вычисляется критическое значение критерия, с которым и будет сравниваться расчетное значение:

,

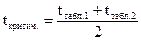где t_{табл. 1} — табличное значение критерия Стьюдента для 1-й выборки;

t_{табл. 2} — табличное значение критерия Стьюдента для 2-й выборки.

Контрольные вопросы:

1. Что такое статистическая гипотеза?

2. В чем состоит различие между направленными и ненаправленными статистическими гипотезами?

3. Какие бывают ошибки при проверке статистических гипотез?

4. Что такое уровень значимости вывода?

5. Каким образом делается вывод при проверке статистических гипотез?

6. Что такое критерий различий?

7. Приведите классификацию критериев различий.

8. В чем различие между односторонними и двусторонними критериями?

9. От чего зависит выбор критерия различий?

10. Назовите условия применения критерия Стьюдента.

11. Какие параметры распределений признаков необходимо знать для того, чтобы рассчитать критерий Стьюдента?

12. Сформулируйте правило принятия решения по результатам расчетов критерия Стьюдента.

13. Почему при расчете критерия Стьюдента необходимо параллельно оценивать и изменчивость признаков в выборках?

14. Каким образом можно сравнить две дисперсии?

15. В каких случаях в правило вывода критерия Стьюдента необходимо вводить поправку Снедекора?

Самостоятельное практическое задание: для каждого критерия различий придумайте пример психологического исследования, в котором статистическую гипотезу необходимо было проверить с помощью данного критерия.

Материалы для изучения темы:

а) основная литература:

1. Ермолаев О. Ю. Математическая статистика для психологов. — М., 2008. — Стр. 58-70.

2. Кутейников А.Н. Математические методы в психологии. – СПб, 2008. — Стр. 50-59.

3. Наследов А. Д. Математические методы психологического исследования: Анализ и интерпретация данных. — СПб., 2007. — Стр. 93-113.

4. Сидоренко Е. В. Методы математической обработки в психологии. — СПб.,2004. — Стр. 24-38.

б) дополнительная литература:

1. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. — М., 1976. — Стр. 246-264.

2. Суходольский Г. В. Основы математической статистики для психологов. — СПб., 1998. — 291-294.

Дата добавления: 2014-12-26