
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод половинного деления
|
|
|
|
Уточнение приближенных корней
Графический метод отделения корней
Действительные корни уравнения f(x)=0 можно определить как абсциссы точек пересечения графика функции  с осью Ох. Если уравнение
с осью Ох. Если уравнение 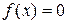 не имеет близких между собой корней, то этим способом корни легко определяются. На практике часто удобно тождественно преобразовать уравнение к виду
не имеет близких между собой корней, то этим способом корни легко определяются. На практике часто удобно тождественно преобразовать уравнение к виду  , где
, где 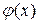 и
и  - более простые функции, чем функция
- более простые функции, чем функция  . Тогда, построив графики
. Тогда, построив графики 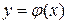 и
и  , искомые корни получаются как абсциссы точек пересечения этих графиков.
, искомые корни получаются как абсциссы точек пересечения этих графиков.
Пример 2.2
Отделить графически корни уравнения x·ln(x) -1=0. Преобразуем уравнение к виду 1/x=ln(x) и построим графики.

|
Рис 2.1. Графический метод отделения корней
Из графика видно, что 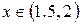 .
.
Пусть уравнение (2.1) имеет на отрезке [ a,b ] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0. Разделим отрезок [ a,b ] пополам точкой x1=(а+b)/2. Если f(x1)≠0, то для продолжения вычислений выберем ту часть промежутка, где знаки функции различны. Концы полученного отрезка обозначим [ a1,b1 ] и снова разделим отрезок [ a1,b1 ] пополам точкой x2=(a1+ b1)/2 и т. д. В результате на каком-то этапе получим или точный корень уравнения(2.1) или бесконечную последовательность вложенных друг в друга отрезков [ a1,b1 ], [ a2,b2 ],… [ an,bn ],…таких, что
f(an)·f(bn)<0, (n=1,2,…) (2.2)
bn - an=2 -n·(b-a). (2.3)
Так как левые концы a1, a2,…,an образуют монотонную неубывающую ограниченную последовательность, а правые концы b1 b2,…,bn образуют монотонную невозрастающую ограниченную последовательность, а расстояние между ними в силу (2.2) стремится к нулю, то у последовательностей существует общий предел. Число ξ, которое является общим пределом последовательностей { an } и { bn }, точный корень уравнения (2.1). Оценим погрешность решения на n -м шаге. Считаем до тех пор, пока длина промежутка не станет меньше заданной точности ε.

В качестве ответа возьмем середину отрезка [ an,bn ].
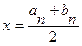 .
.
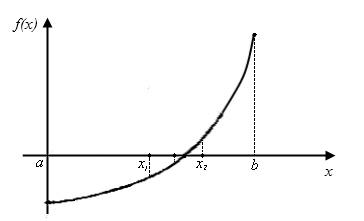
Рис.2.2. К объяснению метода половинного деления
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, так как при увеличении точности значительно возрастает объём вычислений.
Пример 2.3. Найти, используя пакет Matchcad, методом половинного деления корень уравнения x4-x3-2x2+3x-3=0 на промежутке [1,2]
Функция koren(a,b,ε) возвращает длину отрезка, который будет меньше заданной точности ε, и значение корня на этом промежутке, если на концах отрезка [ a,b ] функция имеет противоположные знаки, или сообщение об отсутствии корня, в противном случае.
Метод легко реализуется на компьютере. Далее приводится листинг программы, написанной на языке, встроенном в систему Mathcad.
 Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 754; Нарушение авторских прав?; Мы поможем в написании вашей работы!