Решение дифференциальных уравнений

В общем случае для переходных процессов в линейной электрической цепи с n независимыми реактивными элементами составляется неоднородное дифференциальное уравнение n- го порядка

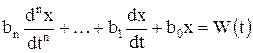, (6.6)

где – независимая переменная (ток или напряжение), 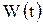– внешнее воздействие, коэффициенты 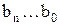определяются параметрами цепи. Решение уравнения (6.6) находится как сумма двух независимых решений

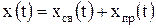, (6.7)

где 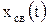– свободная составляющая, являющаяся общим решением однородного дифференциального уравнения [уравнения (6.6) с нулевой правой частью], – принужденная составляющая, частное решение неоднородного уравнения.

Принужденная составляющая находится в установившемся режиме при 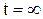(после завершения переходных процессов) с учетом внешнего источника 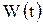. Для расчета применяются такие же методы, что и при определении начальных условий, с учетом нового состояния электрической цепи. Для решения однородного дифференциального уравнения на основе (6.6) составляют характеристическое уравнение

, (6.8)

где оператор 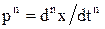. Решением алгебраического уравнения (6.8) являются корни 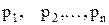, вид которых определяет характер свободной составляющей .

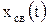Если корни 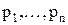вещественные и различные, свободная составляющая представляет собой сумму экспонент

, (6.9)

где постоянные интегрирования находятся из начальных условий.

Для случая вещественных и равных корней решение однородного дифференциального уравнения записывается в виде

. (6.10)

Наиболее интересным является случай комплексно-сопряженных корней 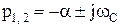. В этом случае каждой паре корней характеристического уравнения в выражении для 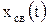соответствует слагаемое

,

где A и Q - постоянные интегрирования, находятся из начальных условий.

Для упрощения решения задач расчета переходных процессов характеристическое уравнение составляется с использованием понятия обобщенного сопротивления цепи , которое получается из комплексного сопротивления заменой jw на оператор p. Комплексное сопротивление определяется для электрической цепи после коммутации при короткозамкнутых источниках ЭДС. Далее одна из ветвей размыкается и относительно места размыкания находится входное сопротивление. Например, для электрической цепи на рис. 6. 5 входное сопротивление

.

Далее после преобразований и замены jw на p получим характеристическое уравнение

.

Дата добавления: 2014-12-26