Спектры некоторых периодических колебаний

Прямоугольное колебание (меандр) изображено на рис. 7.3.

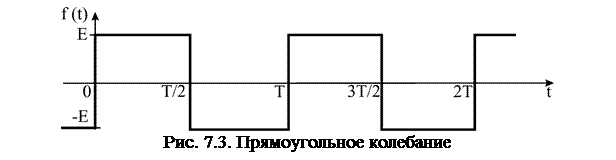При выбранном на рис. 7.3 начале отсчета времени функция 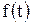является нечетной. Коэффициенты ряда Фурье для нечетных функций a_n=0. Для коэффициентов b_n имеем

.

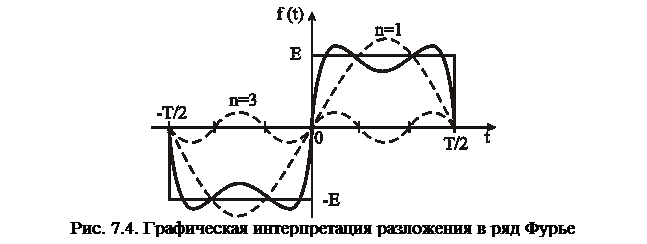
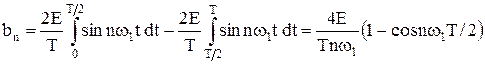Учитывая, что 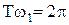, получаем

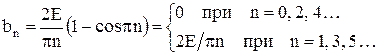(7.5)

Начальные фазы равны 0 для всех гармоник. В тригонометрической форме ряд Фурье для прямоугольного колебания имеет вид

.

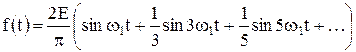Графическая интерпретация ряда Фурье и спектр колебания представлены на рис. 7.4, 7.5. Спектр прямоугольного колебания состоит из бесконечного количества нечетных гармоник. С увеличением числа гармоник сумма ряда приближается к функции 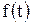. При ограниченном числе гармоник ряд Фурье лишь приближенно аппроксимирует прямоугольное колебание.

Последовательность прямоугольных импульсов (рис. 7.6).

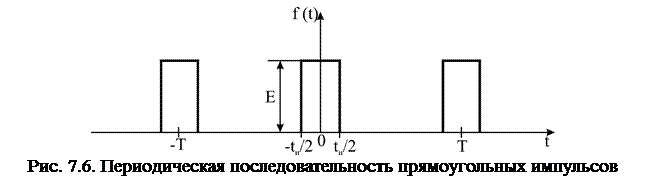
В данном случае функция 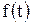четная и коэффициенты ряда Фурье b_n=0.

Значение средней (постоянной) составляющей

.

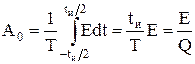Значения коэффициентов ряда Фурье

.

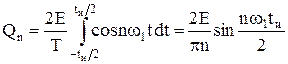Таким образом,

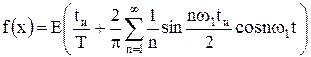. (7.6)

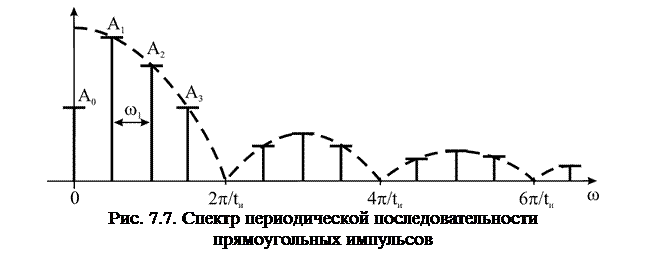
Спектр последовательности прямоугольных импульсов изображен на рис. 7.7.

Спектр состоит из дискретных составляющих, амплитуда 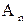которых определяется огибающей вида 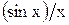, где 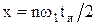. Расстояние между соседними линиями спектра определяется периодом повторения .

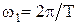Огибающая спектра имеет нули в точках 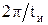, 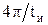и т. д. Спектр состоит из основного лепестка и ряда боковых лепестков. Протяженность основного лепестка 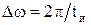принимается за условную ширину спектра. Учитывая, что 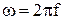, для ширины спектра в Гц получим 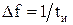. Откуда

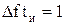. (7.7)

Это фундаментальное соотношение говорит о том, что произведение ширины спектра на длительность импульса остается постоянным. Поэтому более короткие импульсы имеют более широкий спектр.

Число дискретных линий в одном лепестке спектра равно скважности импульсной последовательност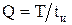и . При 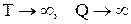периодическая последовательность вырождается в одиночный импульс. При этом расстояние между спектральными линиями и спектр из линейчатого превращается в сплошной, но ширина спектра по-прежнему определяется соотношением (7.7).

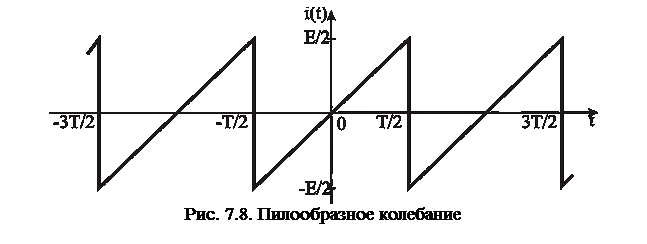Пилообразное колебание используется в устройствах развертки в осциллографах и мониторах. Колебание (график на рис. 7.8) описывается нечетной функцией, и ряд Фурье для нее содержит только синусоидальные члены6

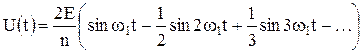. (7.8)

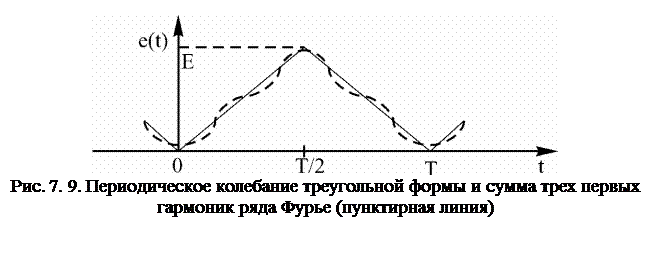
Периодическая последовательность импульсов треугольной формы (рис. 7.9). Один импульс последовательности описывается выражением

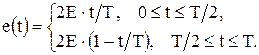
Постоянная составляющая напряжения последовательности импульсов треугольной формы равна

.

Форма этой последовательности импульсов описывается четной функцией, поэтому коэффициенты ряда Фурье a_n=0, а коэффициенты b_n описываются выражением

Ряд Фурье для данной последовательности состоит из суммы постоянной составляющей и нечетных гармоник

.

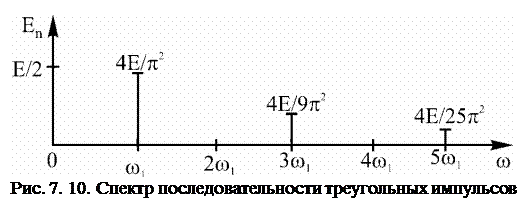
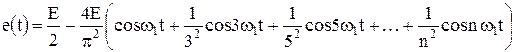Спектральная диаграмма последовательности изображена на рис. 7. 10.

Периодическая последовательность косинусоидальных импульсов. Такая последовательность возникает при воздействии на нелинейные элементы гармонических колебаний. Примером нелинейного элемента может служить полупроводниковый диод, вольт-амперная характеристика которого в первом приближении описывается кусочно-линейной функцией (рис. 7.11).

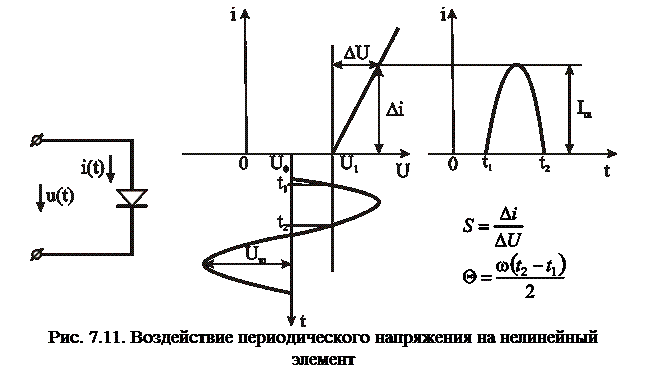
Наклон ВАХ характеризуется крутизной 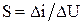. Если к диоду приложить напряжение, состоящее из постоянной и переменной составляющих 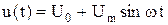, то при определенных соотношениях между величинами 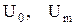и напряжением отсечки диода U₁ ток диода будет иметь форму косинусоидальных импульсов с углом отсечки 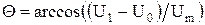. Угол отсечки может изменяться в пределах от 0 (ток диода равен нулю) до 180^° (режим без отсечки тока диода). Ток диода имеет форму периодических импульсов косинусоидальной формы, описываемых выражением

,

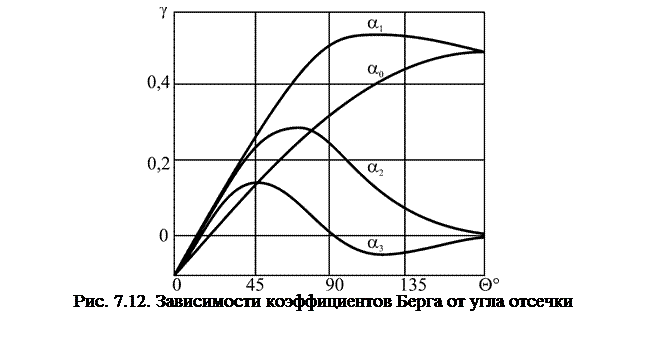
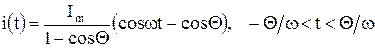где 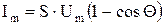– амплитуда импульсов тока.

Коэффициенты ряда Фурье для периодической последовательности косинусоидальных импульсов являются функциями угла отсечки:

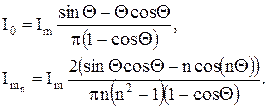(7.9)

Вводят нормированные параметры – коэффициенты Берга:

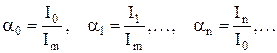
Зависимости первых четырех коэффициентов от угла отсечки приведены на рис. 7.12.

7.4. Расчет электрических цепей несинусоидального тока
с использованием разложения в ряд Фурье

Пусть требуется рассчитать ток в электрической цепи под действием периодической несинусоидальной ЭДС

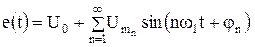, (7.10)

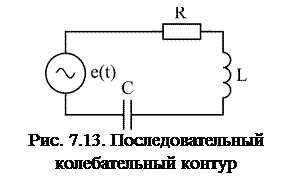
где 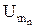– амплитуда n-й гармоники ЭДС. В линейных электрических цепях токи в ветвях находятся методом наложения (суперпозиций), путем суммирования токов, создаваемых каждым из слагаемых ЭДС (7.10). Для случая цепи, состоящей из последовательного соединения R, L, С элементов (рис. 7.13), имеем

,

где – амплитуда n-й гармоники тока,

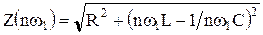– полное сопротивление цепи на частоте , .

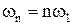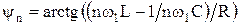Сопротивление цепи на постоянном токе 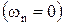равно 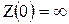, поэтому постоянная составляющая тока 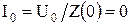. При увеличении номера гармоники, т.е. с увеличением частоты 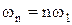, индуктивное сопротивление возрастает 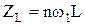, а емкости уменьшаются 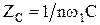, поэтому полное сопротивление цепи является функцией частоты . Если при некотором значении n выполняется условие 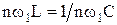, на частоте 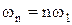возникает резонанс напряжения.

Расчет разветвленной цепи периодического несинусоидального тока ведется для каждой гармоники в символической форме. Полный ток находится суммированием мгновенных значений гармоник тока в ветвях, так как векторы комплексных токов имеют различную частоту вращения.

7.5. Действующее значение и мощность периодического
несинусоидального тока

Действующее значение периодических токов (напряжений) определяется выражением

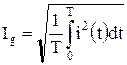. (7.11)

Для синусоидального тока действующее значение тока вычисляется по формуле

.

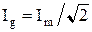В случае периодического несинусоидального тока вычисления по формуле (7.11) с использованием разложения в ряд Фурье дают результат

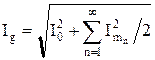. (7.12)

Так как 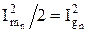– квадрат действующего значения n-й гармоники, (7.12) можно записать в виде

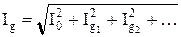. (7.13)

Таким образом, действующее значение периодического несинусоидального тока равно корню квадратному из суммы квадратов действующих значений гармоник, включая постоянную составляющую. Активная мощность периодического несинусоидальго тока также может быть рассчитана с использованием разложения в ряд Фурье. Известно, что активная мощность равна среднему значению мощности за период

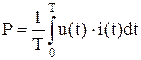. (7.14)

При разложении периодических токов и напряжений в ряд Фурье средняя мощность каждой гармоники рассчитывается по формуле

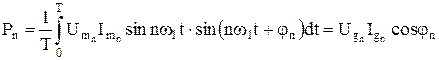, (7.15)

где j_n – сдвиг фазы между током и напряжением n-й гармоники. Интегрирование по формуле (7.14) с учетом ортогональности гармонических функций дает

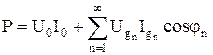. (7.16)

Из (7.16) следует, что активная мощность в цепях периодического несинусоидального тока равна сумме активных мощностей отдельных гармоник и мощности постоянной составляющей. Для несинусоидальных токов также используют такие параметры, как коэффициент формы, коэффициент амплитуды и коэффициент гармоник. Коэффициент формы определяется как отношение действующего значения тока к среднему значению:

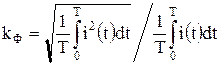. (7.17)

Для синусоидального тока 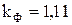. Коэффициент амплитуды определяется как отношение максимального значения к действующему значению:

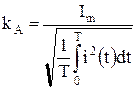. (7.18)

Для синусоидального тока .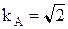

Коэффициент гармоник определяется выражением

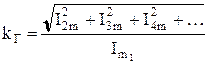. (7.19)

Коэффициент гармоник используется для оценки степени соответствия периодического тока синусоидальному току.

Дата добавления: 2014-12-26