Переходные процессы в электрических цепях II порядка

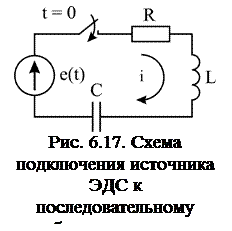
Линейная цепь II порядка содержит два реактивных элемента L и C. Примером электрической цепи II порядка является последовательный колебательный контур (рис. 6.17).

Составим дифференциальное уравнение для переходного процесса:

.

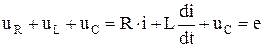Учитывая, что 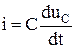, записываем

. (6.18)

Выражение (6.18) является дифференциальным уравнением II порядка. Его решение состоит из свободной и принужденной составляющих

.

Принужденная составляющая зависит от внешнего воздействия 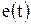и определяется в установившемся режиме при 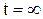. Свободная составляющая 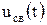является решением однородного дифференциального уравнения

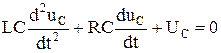. (6.19)

Для определения 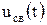составляется характеристическое уравнение, соответствующее дифференциальному уравнению (6.19):

,

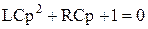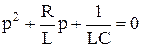. (6.20)

Находятся корни уравнения (6.20):

.

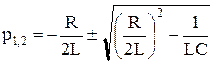Вводятся обозначения: 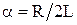– коэффициент затухания, 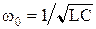– резонансная частота контура. Важным параметром, определяющим характер переходного процесса в колебательных контурах, является добротность

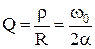, (6.21)

где 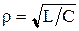– характеристическое сопротивление контура. Используя выражение (6.21), корни характеристического уравнения можно представить в виде

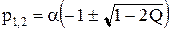. (6.22)

В зависимости от величины добротности могут быть три варианта корней характеристического уравнения и соответственно три вида свободной составляющей переходного процесса.

1. 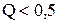, корни действительные и различные, переходный процесс носит апериодический характер: .

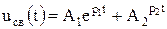2. 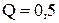, корни действительные, равные, переходный процесс носит промежуточный характер: .

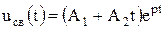3. 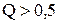, корни комплексно-сопряженные, переходный процесс носит колебательный затухающий характер: ,

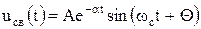где А₁, А₂, А, Q –постоянные интегрирования, находятся из начальных условий, .

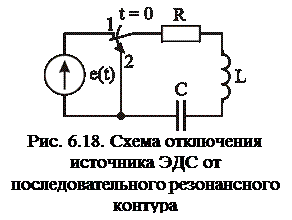
Рассмотрим переходные процессы в последовательном колебательном контуре при разряде емкости на RL цепь (схема на рис. 6.18). До коммутации емкость заряжена до величины 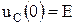(ненулевые начальные условия), ток через индуктивность равен нулю 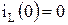(нулевые начальные условия). В конденсаторе запасена энергия 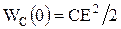. После коммутации (в момент t=0 ключ переводится в положение 2) емкость начинает разряжаться через R, L элементы и в контуре возникает переходный процесс.

Напряжение на конденсаторе во время переходного процесса определяется суммой свободной и принужденной составляющих

.

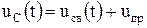Так как после коммутации при 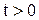источник ЭДС отключается от контура, принужденная составляющая 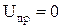, решение дифференциального уравнения состоит только из свободной составляющей

.

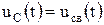Случай 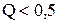, корни характеристического уравнения (6.20) вещественные и различные (p₁<0, p₂<0):

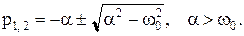
Свободная составляющая для этого случая состоит из двух компонент:

.

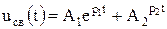Постоянные интегрирования А₁ и А₂ находим из начальных условий. Для использования начального условия для индуктивности 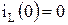определяем выражение для тока в электрической цепи

.

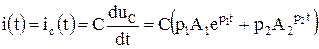Подставляя при t=0 начальные условия для u_C(0) и i_L(0), получаем

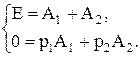
Решая полученную систему уравнений, определяем значения постоянных интегрирования

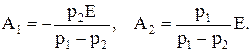
Тогда напряжение на емкости во время переходного процесса будет описываться выражением

,

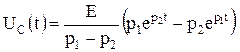а ток в контуре

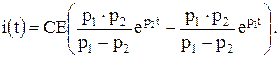
Учитывая, что

,

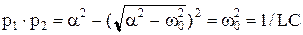получаем

.

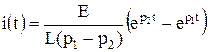Используя выражение для тока 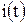, можно рассчитать

.

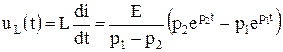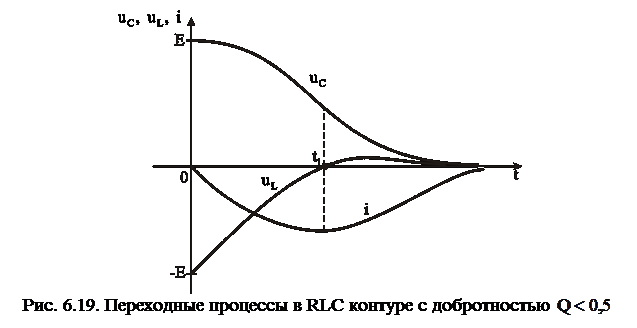
Временные диаграммы напряжений и тока в контуре во время переходных процессов приведены на рис. 6.19. На интервале 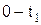происходит разряд конденсатора и заряд индуктивности, далее при 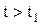конденсатор и индуктивность разряжаются. В течение всего интервала 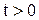через резистор R протекает ток и запасенная в реактивных элементах энергия постепенно расходуется до нуля. Так как напряжение на конденсаторе при его разряде изменяется монотонно (без колебаний), переходный процесс называют апериодическим.

Случай 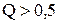(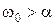), корни характеристического уравнения комплексно-сопряженные:

,

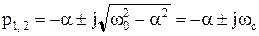где – частота собственных колебаний контура. Решение однородного дифференциального уравнения для этого случая записывается в виде

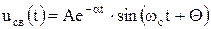, (6.23)

где A и Q – постоянные интегрирования. Для их определения начальные условия подставляются в выражения для напряжения на емкости (6.20) и тока через индуктивность

.

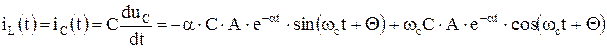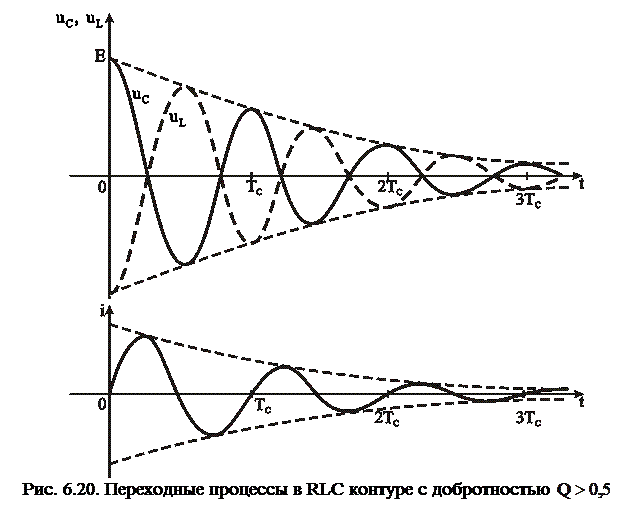При 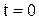имеем

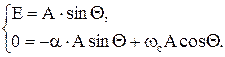
Решая систему уравнений, находим

.

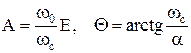При больших добротностях 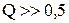постоянная интегрирования 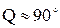и приближенно выражения для напряжений и токов во время переходного процесса можно записать в виде

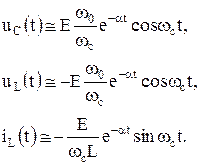
Временные диаграммы напряжений на реактивных элементах С и L и тока в контуре показаны на рис. 6.20.

В контуре во время переходных процессов имеет место колебательный процесс обмена энергией между емкостью и индуктивностью с частотой . Интервал T=2π/w_c называют квазипериодом колебаний. Перезарядный ток i(t) протекает через сопротивление R, и часть энергии, сосредоточенной в реактивных элементах, расходуется, поэтому переходный процесс имеет затухающий характер. Затухание происходит по экспоненциальному закону с коэффициентом затухания 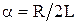. Чем больше сопротивление R, тем больше коэффициент затухания и тем быстрее завершается переходный процесс. При , когда 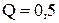, переходный процесс из колебательного превращается в апериодический. Теоретически можно представить себе контур без потерь с 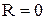, в котором существуют незатухающие колебания с частотой . В контуре без потерь имеет место переменный обмен энергией между С и L, при котором энергия электрического поля конденсатора преобразуется в энергию магнитного поля индуктивности, а затем наоборот. В реальных электрических цепях R>0, поэтому переходный процесс имеет затухающий характер.

Рассмотрим переходные процессы при подключении источника постоянной ЭДС к параллельному колебательному контуру (схема на рис. 6.21).

За независимую переменную при анализе переходных процессов в схемах с параллельным соединением L и С принимают ток через индуктивность 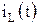. В исходном состоянии при 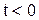источник ЭДС отключен от контура, 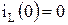, , 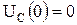начальные условия нулевые. Для составления характеристического уравнения найдем входное сопротивление цепи после коммутации

.

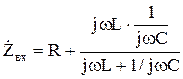После введения параметра 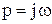и преобразований получим характеристическое уравнение вида

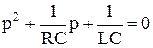. (6.24)

Корни характеристического уравнения имеют вид

.

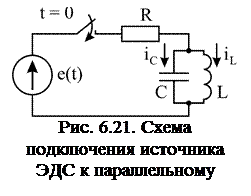
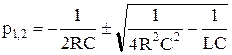Добротность параллельного контура определяется выражением

,

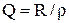где 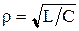– характеристическое сопротивление контура. При 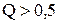корни уравнения (6.24) комплексно-сопряженные:

,

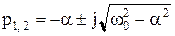где 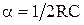– коэффициент затухания.

Следует заметить, что в параллельном контуре, по схеме рис. 6.21, в отличие от последовательного контура (рис. 6.17) при увеличении сопротивления R затухание уменьшается, а добротность контура увеличивается.

Принужденная составляющая тока через индуктивность определяется после завершения переходных процессов при :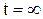

.

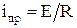Для случая 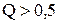изменение тока через индуктивность во время переходного процесса будет описываться функцией

.

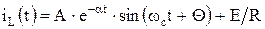После дифференцирования тока 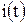находим напряжение на индуктивности, которое равно напряжению на емкости:

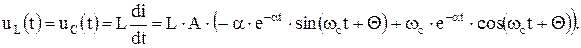
Подставляем в выражения для тока 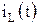и напряжения 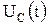начальные значения при 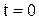, получаем систему уравнений

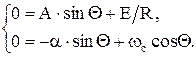
Решением системы уравнений являются постоянные интегрирования

.

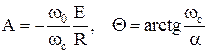Тогда для тока в цепи во время переходных процессов запишем выражение

.

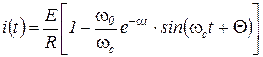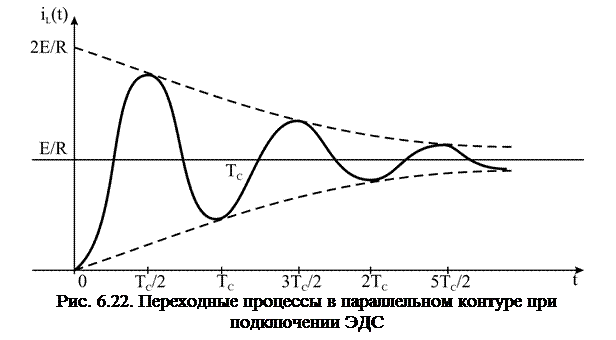График изменения тока при добротности Q>>1, когда Q=90, показан на рис. 6.22.

В исходном состоянии индуктивность и емкость разряжены: 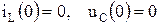. После замыкания ключа начинается заряд L и С через резистор. Причем в соответствии с законами коммутации ток через индуктивности нарастает плавно, а ток через емкость в момент 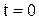скачком увеличивается до величины 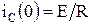, а затем плавно изменяется. После коммутации имеет место периодический обмен энергией между L и С и переходный процесс носит колебательный характер.

Дата добавления: 2014-12-26