Общие сведения. Несинусоидального тока

Несинусоидального тока

Электрические цепи периодического

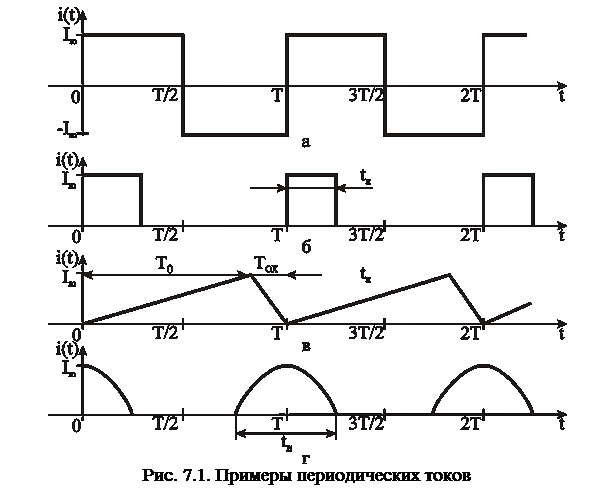В электротехнике и электронике наряду с переменными синусоидальными токами и напряжениями применяются периодические токи и напряжения других форм. Примеры таких токов показаны на рис. 7.1. Прямоугольное колебание – меандр (рис. 7.1, а) является дискретным аналогом гармонического колебания. Меандр характеризуется амплитудой колебания 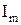и периодом Т. С периодом связана частота колебаний 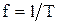[Гц]. Наиболее распространенным видом периодического несинусоидального тока является последовательность прямоугольных импульсов (рис. 7.1, б), которая характеризуется амплитудой 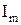, периодом Т (частотой 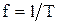) и длительностью импульсов 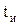, а также скважностью 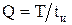. На рис. 7.1, в изображена последовательность пилообразных импульсов. Кроме амплитуды 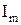и периода Т параметрами пилообразного тока являются длительность прямого Т₀ и обратного хода Т_ох. К периодическим несинусоидальным колебаниям относится также последовательность косинусоидальных импульсов (рис. 7.1, г), для которых вводится дополнительный параметр – угол отсечки .

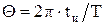Для расчета электрических цепей с источниками периодического несинусоидального тока или напряжения символический метод расчета цепей синусоидального тока непосредственно неприменим. Однако, раскладывая периодические несинусоидальные ЭДС на сумму синусоидальных составляющих (на сумму гармоник) и используя принцип суперпозиции, для расчета линейных электрических цепей несинусоидального тока можно использовать символический метод. Процедура расчета в этом случае состоит в разложении периодических несинусоидальных ЭДС на ряд синусоидальных ЭДС и расчете электрической цепи для каждой гармонической составляющей с последующим суммированием результатов расчета для каждой отдельной гармоники.

Дата добавления: 2014-12-26