Примеры линейных четырехполюсников

Идеальный фильтр низких частот ФНЧ – используется как идеализированная модель реальных фильтров. Комплексный коэффициент передачи идеального ФНЧ описывается функцией вида

(8.13)

где W_ср – частота среза фильтра. АЧХ и ФЧХ идеального фильтра показаны на рис. 8.8. Коэффициент передачи идеального ФНЧ в полосе прозрачности 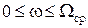равен постоянной величине К₀, а в полосе задержания 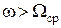равен 0. Фазочастотная характеристика идеального ФНЧ в полосе прозрачности описывается линейной функцией.

Используя (8.11) и (8.13), определяем импульсную характеристику идеального фильтра нижних частот.

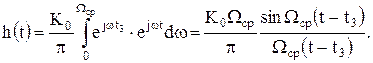(8.14)

Входное воздействие в виде дельта-функции и импульсная характеристика идеального фильтра ФНЧ показаны на рис. 8.9

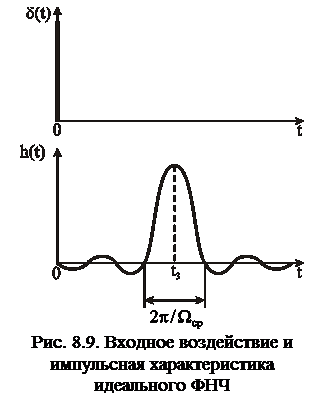Импульсная характеристика идеального ФНЧ описывается функцией вида 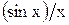, где 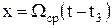. Длительность главного максимума импульсной характеристики зависит от частоты среза. Чем больше частота среза, тем короче импульсная реакция ФНЧ. Переходная характеристика фильтра может быть определена как интеграл от импульсной характеристики:

,

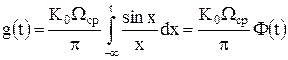где 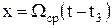, 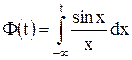– интегральный синус, табулированная функция.

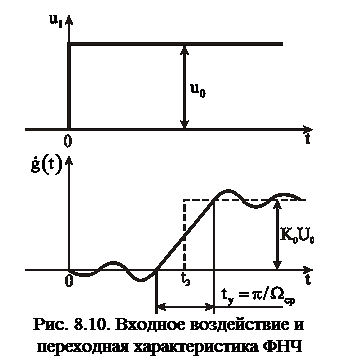
Входное воздействие в виде единичного скачка напряжения и переходная характеристика идеального ФНЧ показаны на рис. 8.10.

При скачкообразном изменении напряжения на входе фильтра выходное напряжение изменяется с конечной скоростью, определяемой частотой среза. Для переходной характеристики вводят параметр – время установления t_у – это интервал, в течение которого напряжение на выходе изменяется от нулевого уровня до уровня установления:

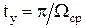. (8.15)

Чем выше частота среза, тем меньше время установления. Как видно из рис. 8.10, переходный процесс в идеальном ФНЧ носит колебательный характер.

Интегрирующая RС цепочка может рассматриваться как линейный четырехполюсник (рис. 8.11). Комплексный коэффициент передачи определяется как

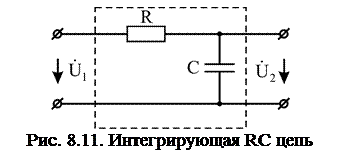
. (8.16)

Интегрирующая RС цепочка характеризуется параметром 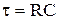– постоянной времени. Из (8.16) находим АЧХ и ФЧХ интегрирующей цепочки:

. (8.17)

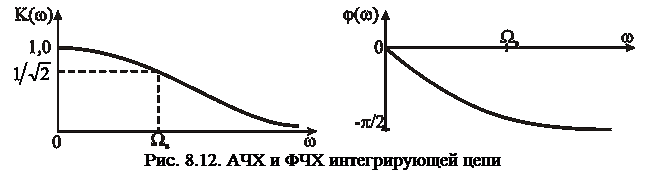
Частотные характеристики цепочки показаны на рис. 8.12.

Частота W_ср, на которой коэффициент передачи снижается до уровня , называется верхней:

. (8.18)

Переходная характеристика цепочки определяется с помощью соотношения (8.11)

. (8.19)

Переходная характеристика описывается экспоненциальной функцией (рис. 8.13), что соответствует характеру переходных процессов в линейных цепях I порядка. Время установления переходной характеристики, определенное по уровням 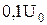и , вычисляется по формуле

. (8.20)

Следует отметить, что интегрирующая цепочка является фильтром нижних частот I порядка с частотой среза .

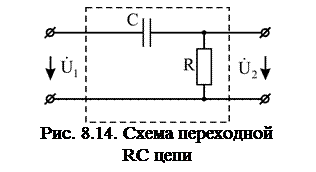
Переходная RС цепочка (рис. 8.14).

Находим комплексный коэффициент передачи переходной цепочки

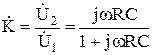. (8.21)

АЧХ и ФЧХ цепочки описываются выражениями

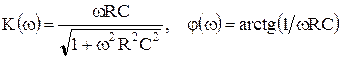. (8.22)

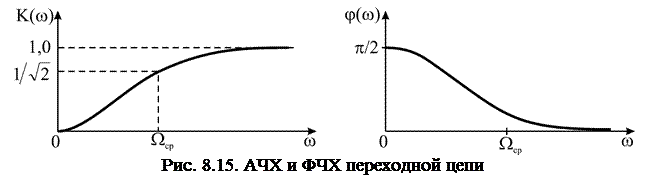
Параметром цепочки является 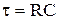– постоянная времени. АЧХ и ФЧХ переходной цепочки показаны на рис. 8.15.

Переходная цепочка является фильтром верхних частот I порядка с частотой среза .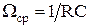

Переходная характеристика цепочки описывается экспоненциальной функцией

. (8.23)

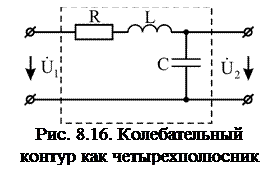Последовательный колебательный контур может использоваться как четырехполюсник (рис. 8.16) и в зависимости от добротности Q иметь различные частотные характеристики. Комплексный коэффициент передачи описывается выражением

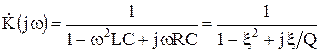, (3.24)

где 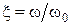– нормированная частота, 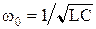– резонансная частота контура, 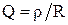– добротность контура.

АЧХ контура при нескольких значениях добротности показаны на рис. 8.17

При низких добротностях АЧХ приближается к характеристике интегрирующей цепочки, а при 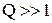имеет вид резонансной кривой. При добротностях 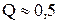RLС цепь может использоваться как ФНЧ II порядка.

Дата добавления: 2014-12-26