Переходные процессы в электрических цепях I порядка

Электрические цепи I порядка содержат один реактивный элемент и одно или несколько сопротивлений (RL и RC цепи). Они могут выполнять функции интегрирующих дифференцирующих цепочек.

Переходные процессы в них описываются дифференциальными уравнениями I порядка. Рассмотрим случаи подключения и отключения источников ЭДС к RL и RC цепям.

Подключение источника ЭДС к RL цепи (рис. 6. 6).

До момента коммутации при t<0 источник ЭДС отключен от электрической цепи, начальные условия нулевые . В качестве независимой переменной принимаем ток через индуктивность 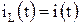. Составим дифференциальное уравнение.

. (6.11)

Решение дифференциального уравнения находится в виде суммы свободной и принужденной составляющих:

. (6.12)

Свободная составляющая является общим решением однородного дифференциального уравнения:

. (6.13)

Для дифференциальных уравнений 1-го порядка это решение имеет вид

,

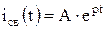где р – корень характеристического уравнения

,

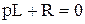откуда

[1/с].

Вводят новый параметр цепи – постоянную времени

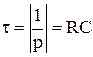[c].

При подключении к цепи источника постоянного напряжения принужденная составляющая находится из схемы после коммутации (рис. 6.7)

.

Запишем решение уравнения (6.7) в виде суммы свободной и принужденной составляющих

. (6.14)

Для нахождения постоянной интегрирования А используем начальное условие . Из (6.14) при 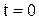имеем

,

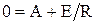откуда

.

Тогда для тока в цепи во время переходных процессов окончательно запишем

. (6.15)

Для нахождения напряжения на индуктивности используем закон Фарадея

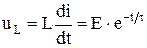. (6.16)

Напряжение на сопротивлении находится по закону Ома:

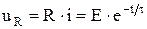. (6.17)

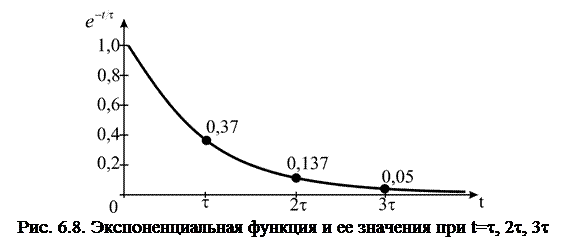
Из выражений (6.15), (6.16), (6.17) следует, что переходные процессы в RL цепи протекают по экспоненциальному закону с постоянной времени 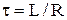. Скорость переходных процессов определяется величиной постоянной времени t, чем больше t, тем медленнее протекают переходные процессы (рис. 6.8)

Переходные процессы принято изображать в виде временных диаграмм – зависимостей тока и напряжений от времени. Временные диаграммы, построенные по формулам (6.15), (6.16), (6.17), приведены на рис. 6.9. Подключение

источника постоянной ЭДС можно рассматривать как воздействие на электрическую цепь напряжения вида , где 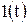– единичная функция (функция включения). До момента коммутации 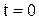индуктивность разряжена, так как ток . При подключении источника ЭДС начинается процесс заряда индуктивности, ток возрастает по экспоненциальному закону, стремясь при 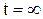к установившемуся значению . В момент коммутации напряжение на индуктивности скачком изменяется до величины Е и по мере заряда индуктивности спадает по экспоненциальному закону. Напряжение на сопротивлении по форме совпадает с током 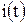, так как . Когда переходные процессы завершаются, ток в

цепи достигает наибольшего значения , в индуктивности будет запасена энергия .

При подключении к электрической цепи источника синусоидального напряжения в решении (6.15) дифференциального уравнения (6.14) изменяется только принужденная составляющая, которая рассчитывается символическим методом в соответствии со схемой электрической цепи в установившемся режиме после коммутации (рис. 6.10):

,

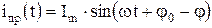где .

Тогда выражение для тока в цепи в течение переходных процессов принимает вид

.

Используя начальное условие , определяем значение постоянной интегрирования:

.

Окончательно для тока в цепи записываем

.

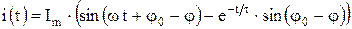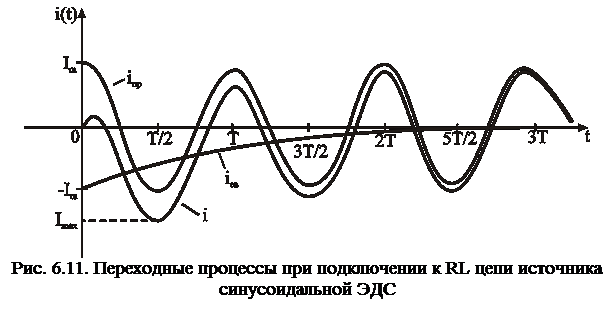
Временная диаграмма тока показана на рис. 6.11. Из него видно, что во время переходных процессов, возникающих при подключении нагрузок, в электрических цепях переменного тока возникают сверхтоки . При больших постоянных времени мгновенные значения токов могут превышать амплитудное значение почти в два раза.

Отключение RL цепи от источника ЭДС.

Схема электрической цепи для этого случая представлена на рис. 6.12. В исходном состоянии до момента коммутации через индуктивность протекает ток .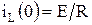

В индуктивности запасена энергия . После коммутации и завершения переходных процессов индуктивность полностью разряжается через сопротивление R и ее ток 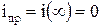. Поэтому решение дифференциального уравнения будет состоять только из свободной составляющей.

.

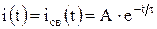Используя начальное условие 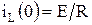, находим постоянную интегрирования

A=E/R

и записываем выражение для тока в цепи во время переходных процессов

.

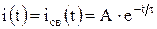Далее находим напряжение на индуктивности и сопротивлении

Диаграммы переходного процесса при отключении источника ЭДС от RL цепи показаны на рис. 6.13.

Подключение источника ЭДС к RC цепи.

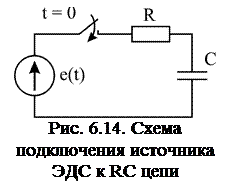
Схема электрической цепи для этого случая показана на рис. 6.14. Источник ЭДС в исходном состоянии при 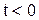отключен от цепи, начальные условия нулевые 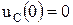. В качестве независимой переменной принимается напряжение на конденсаторе и составляется дифференциальное уравнение

.

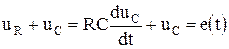Записываем характеристическое уравнение

и находим его корень .

В качестве параметра RC цепи используют постоянную времени [c].

Свободная составляющая переходного процесса описывается экспоненциальной функцией

.

При подключении источника постоянной ЭДС принужденная составляющая 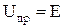, так как после завершения переходных процессов конденсатор заряжается до напряжения источника ЭДС. Тогда переходный процесс будет описываться функцией

.

Используя начальное условие 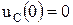, определяем значение постоянной интегрирования 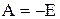и окончательно записываем

.

Ток в цепи во время переходного процесса

.

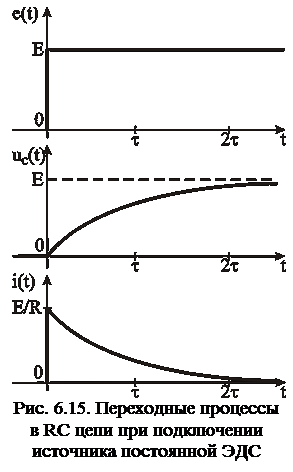
Временные диаграммы переходного процесса в RC цепи при подключении постоянной ЭДС показаны на рис. 6.15. Во время переходного процесса происходит заряд емкости С от источника ЭДС через сопротивление R. В емкости запасается энергия 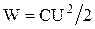. Такая же энергия расходуется при протекании зарядного тока через сопротивление. Скорость заряда зависит от постоянной времени t. С увеличением t инерционность цепи увеличивается и заряд конденсатора происходит медленнее.

При отключении цепи от источника в схеме (рис. 6.16) происходит обратный процесс разряда конденсатора С через резистор R. В исходном состоянии при 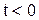конденсатор заряжен до напряжения источника ЭДС , а после завершения переходных процессов разряжается до нуля 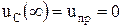. Тогда выражения для напряжения и тока во время переходного процесса примут вид

Подводя итог рассмотрению переходных процессов в линейных цепях I порядка, можно сделать следующие выводы:

1. Переходные процессы описываются дифференциальными уравнениями I порядка.

2. Переходные процессы протекают в соответствии с экспоненциальным законом.

3. Скорость переходных процессов определяется постоянной времени электрической цепи.

Дата добавления: 2014-12-26