
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы уравнений четырехполюсников
|
|
|
|
Линейные четырехполюсники
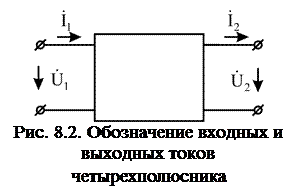
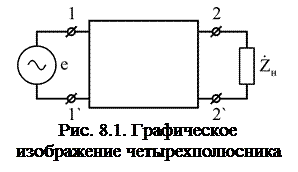 Электрическая цепь, имеющая две пары зажимов, называется четырехполюсником. Понятием четырехполюсника пользуются в тех случаях, когда необходимо знать токи и напряжения только в двух ветвях электрической цепи. Как четырехполюсники рассматриваются электрические фильтры, трансформаторы, длинные линии и др. Изображение четырехполюсника на схемах электрических цепей показано на рис. 8.1.
Электрическая цепь, имеющая две пары зажимов, называется четырехполюсником. Понятием четырехполюсника пользуются в тех случаях, когда необходимо знать токи и напряжения только в двух ветвях электрической цепи. Как четырехполюсники рассматриваются электрические фильтры, трансформаторы, длинные линии и др. Изображение четырехполюсника на схемах электрических цепей показано на рис. 8.1.
К входным зажимам 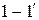 подключается источник электрической энергии, к выходным – нагрузка. Часто один входной и один выходной зажимы соединяют между собой (зажимы
подключается источник электрической энергии, к выходным – нагрузка. Часто один входной и один выходной зажимы соединяют между собой (зажимы 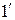 и
и 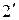 ) и называют общим зажимом.
) и называют общим зажимом.
Четырехполюсники могут быть линейными и нелинейными, активными и пассивными. Ниже рассматриваются линейные четырехполюсники, все элементы которых имеют линейные ВАХ. Активные четырехполюсники содержат источники электрической энергии, пассивные состоят только из нагрузок. Смысл использования четырехполюсников заключается в том, что сложная электрическая цепь может быть представлена с помощью небольшого набора обобщенных параметров. Пассивные четырехполюсники могут быть характеризованы всего тремя независимыми параметрами.
Обозначения направлений входных и выходных токов и напряжений показаны на рис. 8.2.
Напряжения и токи создаются подключением к одной или двум парам зажимов четырехполюсника активных цепей. При этом соотношения между токами и напряжениями на выходе и входе четырехполюсника устанавливаются системой двух уравнений. Существует шесть вариантов записи системы «Z» и «Y» уравнений. Наиболее распространенными являются системы «Z» и «Y» параметров. Уравнения в системе «Z» параметров:
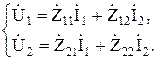 (8.1)
(8.1)
Уравнения в системе «Y» параметров
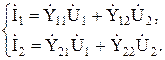 (8.2)
(8.2)
Коэффициенты в уравнениях (8.2) представляют собой входные, выходные и передаточные проводимости:
 – входная проводимость при режиме короткого замыкания на выходе;
– входная проводимость при режиме короткого замыкания на выходе;
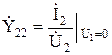 – выходная проводимость при режиме короткого замыкания на входе;
– выходная проводимость при режиме короткого замыкания на входе;
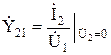 – передаточная проводимость со входа на выход при режиме короткого замыкания на выходе;
– передаточная проводимость со входа на выход при режиме короткого замыкания на выходе;
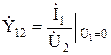 – передаточная проводимость с выхода на вход при режиме короткого замыкания на входе.
– передаточная проводимость с выхода на вход при режиме короткого замыкания на входе.
Если 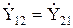 , четырехполюсник является обратимым, если
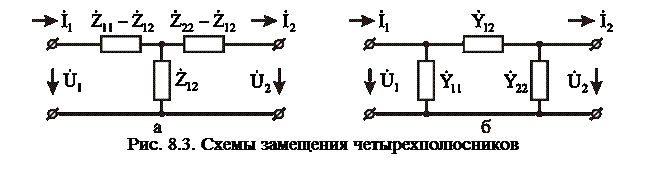
, четырехполюсник является обратимым, если 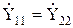 – симметричным. Симметричный четырехполюсник является обратимым. Системам уравнений (8.1) и (8.2) соответствуют эквивалентные схемы пассивных четырехполюсников на рисунках 8.3, а и б.
– симметричным. Симметричный четырехполюсник является обратимым. Системам уравнений (8.1) и (8.2) соответствуют эквивалентные схемы пассивных четырехполюсников на рисунках 8.3, а и б.
Четырехполюсники могут соединяться между собой различными способами. Наиболее распространенные способы соединения – последовательный, параллельный и каскадный – показаны на рис. 8. 4, а, б и в.
Соединения четырехполюсников можно рассматривать как новый четырехполюсник с эквивалентными параметрами, которые определяются при последовательном соединении суммированием соответствующих Z параметров, а при параллельном соединении суммированием Y параметров исходных четырехполюсников. Важными параметрами четырехполюсников являются коэффициенты передачи по току и напряжению и входное сопротивление, определяемые как
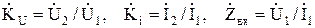 . (8.3)
. (8.3)
Эти параметры могут быть выражены через исходные параметры четырехполюсников ( ,
, 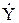 или другие) и сопротивление нагрузки
или другие) и сопротивление нагрузки 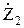 . Например, входное сопротивление через Z параметры, выраженное из системы уравнений (8.1), вычисляется по формуле
. Например, входное сопротивление через Z параметры, выраженное из системы уравнений (8.1), вычисляется по формуле
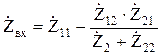 . (8.4)
. (8.4)
8.2. Характеристики линейных четырехполюсников
Характеризуют передачу воздействия от входа к выходу электрической цепи. Чаще всего используют передаточную характеристику по напряжению
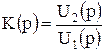 ,
,
где р – некоторый оператор. Если в качестве оператора рассматривают 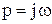 , функция
, функция 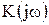 принимает смысл комплексной частотной характеристики четырехполюсника
принимает смысл комплексной частотной характеристики четырехполюсника

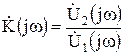 . (8.5)
. (8.5)
Комплексную характеристику (коэффициент передачи) можно представить в виде
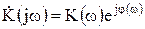 , (8.6)
, (8.6)
где 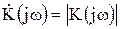 – называется амплитудно-частотной характеристикой (АЧХ),
– называется амплитудно-частотной характеристикой (АЧХ), 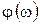 – фазочастотной характеристикой (ФЧХ) четырехполюсника. АЧХ – это зависимость коэффициента передачи четырехполюсника от частоты при воздействии на входе гармонического напряжения (тока). Если входное напряжение линейного четырехполюсника гармоническое:
– фазочастотной характеристикой (ФЧХ) четырехполюсника. АЧХ – это зависимость коэффициента передачи четырехполюсника от частоты при воздействии на входе гармонического напряжения (тока). Если входное напряжение линейного четырехполюсника гармоническое:
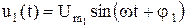 ,
,
то выходное напряжение также является гармоническим с той же частотой и другими значениями амплитуды 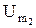 и фазы
и фазы 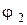 :
:
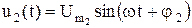 .
.
Тогда АЧХ и ФЧХ, как зависимости от частоты, определяются соотношениями
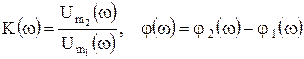 . (8.7)
. (8.7)
Экспериментально АЧХ четырехполюсника измеряется путем изменения частоты входного гармонического напряжения при постоянной амплитуде входного напряжения 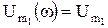 . При этом нормированная зависимость выходного напряжения от частоты
. При этом нормированная зависимость выходного напряжения от частоты 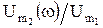 будет являться АЧХ четырехполюсника.
будет являться АЧХ четырехполюсника.
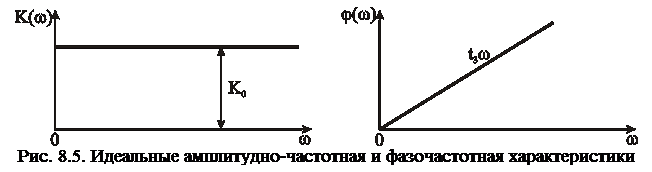
Существует понятие идеального четырехполюсника, АЧХ которого постоянная, а ФЧХ является линейной функцией (рис. 8.5).
При передаче через идеальные четырехполюсники напряжений (токов) их форма не изменяется, а происходит лишь сдвиг во времени на величину 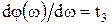 . Реальные четырехполюсники содержат один или несколько реактивных элементов и их АЧХ и ФЧХ отличаются от идеальных. В этом случае форма выходной реакции четырехполюсника не будет совпадать с формой входного воздействия. Для расчета выходной реакции u2(t) четырехполюсника с заданным комплексным коэффициентом передачи
. Реальные четырехполюсники содержат один или несколько реактивных элементов и их АЧХ и ФЧХ отличаются от идеальных. В этом случае форма выходной реакции четырехполюсника не будет совпадать с формой входного воздействия. Для расчета выходной реакции u2(t) четырехполюсника с заданным комплексным коэффициентом передачи 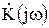 по известному входному воздействию u1(t) можно использовать спектральный метод, основанный на свойствах преобразования Фурье.
по известному входному воздействию u1(t) можно использовать спектральный метод, основанный на свойствах преобразования Фурье.
Известно, что для непериодических функций с помощью прямого преобразования Фурье можно определить спектральную функцию вида
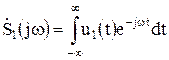 . (8.8)
. (8.8)
Спектральная функция 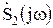 выходной реакции
выходной реакции 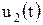 при прохождении воздействия u1(t) через линейный четырехполюсник с комплексным коэффициентом передачи
при прохождении воздействия u1(t) через линейный четырехполюсник с комплексным коэффициентом передачи 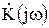 находится как произведение:
находится как произведение:
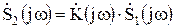 . (8.9)
. (8.9)
Выходная реакция четырехполюсника находится с помощью обратного преобразования Фурье
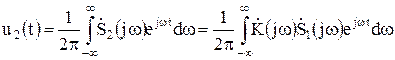 . (8.10)
. (8.10)
АЧХ и ФЧХ определяют свойства линейных четырехполюсников в частной области. Те же свойства во временной области описываются с помощью импульсных и переходных характеристик.
 Импульсной характеристикой
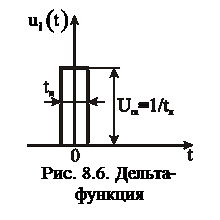
Импульсной характеристикой  называют реакцию линейной цепи на воздействие типа дельта-функции
называют реакцию линейной цепи на воздействие типа дельта-функции 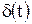 . Дельта-функция (рис. 8.6) – это идеализированное воздействие, которое можно получить из прямоугольного импульса, если устремить длительность импульса
. Дельта-функция (рис. 8.6) – это идеализированное воздействие, которое можно получить из прямоугольного импульса, если устремить длительность импульса 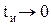 . При этом амплитуда импульса
. При этом амплитуда импульса 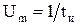 стремится к ¥, а площадь
стремится к ¥, а площадь 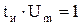 .
.
 Математически показано, что спектральная функция дельта-функции
Математически показано, что спектральная функция дельта-функции 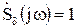 . Тогда в соответствии с (8.10) импульсная характеристика определится как
. Тогда в соответствии с (8.10) импульсная характеристика определится как
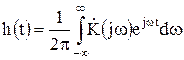 . (8.11)
. (8.11)
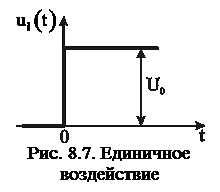
Переходной характеристикой 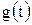 линейных четырехполюсников называется реакция на одиночное воздействие (на скачок напряжения, рис. 8.7).
линейных четырехполюсников называется реакция на одиночное воздействие (на скачок напряжения, рис. 8.7).
Единичное воздействие записывается через единичную функцию
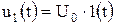 .
.
Спектральная плотность единичного воздействия 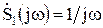 . Тогда в соответствии с (8.9) спектральная функция переходной характеристики равна
. Тогда в соответствии с (8.9) спектральная функция переходной характеристики равна 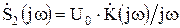 . Используя обратное преобразование Фурье (8.10), для переходной характеристики получим
. Используя обратное преобразование Фурье (8.10), для переходной характеристики получим
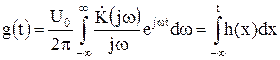 . (8.12)
. (8.12)
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 3256; Нарушение авторских прав?; Мы поможем в написании вашей работы!