Работа и теплота процесса

Как отмечалось выше, работа и теплота представляют собой две различные формы обмена энергией.

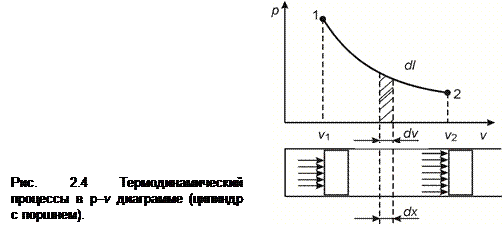
2.3.1 Работа. Рассмотрим равновесный процесс расширения газа в цилиндре с поршнем. Пусть изменение состояния газа в цилиндре изображается в координатах р, υ кривой 1-2 (рис. 2.4). Газ, расширяясь, совершает работу против внешних сил. Нетрудно видеть, что при бесконечно малом перемещении поршня на расстояние dx работа, совершаемая газом, равна:

dL = p·F·dx = p·dV,

где F - площадь поршня, а работа, совершаемая газом в процессе 1-2. Полная работа, совершаемая газом в процессе 1-2, вычисляется из уравнения .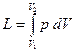

Для 1 кг газа удельная работа равна:

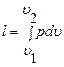, (2.10)

а в элементарном процессе:

dl = p·dυ, (2.11)

где υ – удельный объем. Очевидно, что удельная работа l в p−υ координатах, эквивалентна площади υ ₁ -1-2-υ ₂, расположенной под кривой термодинамического процесса 1-2.

В термодинамике газовых потоков принято следующее правило знаков: работа, совершаемая рабочим телом над внешней средой (работа расширения, dυ > 0), считается положительной, а работа, совершаемая внешней средой над рабочим телом (работа сжатия, dυ < 0) – отрицательной.

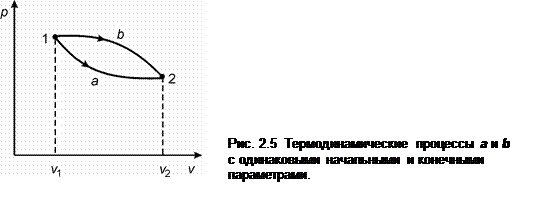
Рассмотрим два процесса перехода тела из состояния 1 в состояние 2 (рис. 2.5). Хотя в процессах a и b исходные и конечные состояния тела одинаковы, но величина работы в этих процессах различна. Таким образом, величина работы зависит от пути процесса, т.е. она является функцией процесса. С учетом (2.11) уравнение первого закона термодинамики можно представить так:

dq = du + p·dυ, (2.12)

а для идеального газа с учетом (2.9):

dq = c_υ · dT + p·dυ. (2.13)

Аналогичные выражения можно получить и для уравнений первого закона термодинамики в интегральной форме.

2.3.2 Теплота. Так как удельная работа l зависит от пути процесса, а величина Δ u не зависит от него, то из (2.2) следует, что теплота является функцией процесса, т.е. ее величина зависит от пути термодинамического процесса. В термодинамике газовых потоков принято следующее правило знаков: теплота, подведенная к телу, считается положительной, а отведенная от него – отрицательной.

Определение количества теплоты – важный элемент расчета термодинамического процесса. Наиболее просто эта задача решается при постоянной теплоемкости процесса:

q = c· (T ₂ – T ₁). (2.14)

В случае переменной теплоемкости возможны различные способы расчета.

Расчет с помощью формул теплоемкости. Из (1.5) следует:

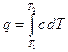. (2.15)

Подставив значение истинной теплоемкости c = a + b·t + d·t ² в уравнение (2.15) и проинтегрировав его, получим

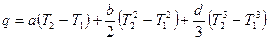. (2.16)

Расчет с использованием значений средних теплоемкостей. Из (1.6) следует:

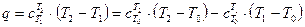
Если перейти от градусов Кельвина к градусам Цельсия и использовать в качестве начального значения температуру t₀ = 0ºC, то будем иметь:

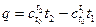. (2.17)

Для расчета по уравнению (2.17) необходимы данные по средним значениям теплоемкости 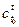, которые представлены в виде таблиц, графиков и т.д.

Расчет с использованием истинной теплоемкости. Для многих газов в достаточно широком интервале температур зависимость теплоемкости от температуры является практически линейной: c = a + b T. Подставив это уравнение в (2.15) и проинтегрировав его, получим:

,

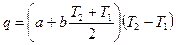Здесь первый сомножитель представляет собой истинную теплоемкость при средней температуре Т _ср. = 0,5(Т ₂ + Т₁). Следовательно, в данном случае теплота может быть найдена по формуле:

q = c _Тср. (T ₂ – T ₁), (2.18)

где c _Тср. – истинная теплоемкость при температуре Т_ср. Указанные способы учета переменности теплоемкости могут быть использованы не только для определения величины q, но и для нахождения других величин, например, изменения внутренней энергии.

В заключение отметим, что при определении теплоты процесса следует использовать величину теплоемкости, которая соответствует данному процессу. Например, для процесса p = const при постоянной теплоемкости имеем: q = c_р (T ₂ - T ₁), а для процесса υ = const: q = c_υ (T ₂ - T ₁).

Дата добавления: 2014-12-27