Нормальные уравнения МНК для некоторых функций

Функции	Нормальные уравнения
y = a+bx	an + b ∑ x = ∑ у; a ∑ + b ∑ х^2 = ∑ ху
у = аЬ^xс^x2	n lg a + lg b ∑ x + lg с ∑ х^2 = ∑lg y lg a ∑ x + lg b ∑ x^2 + lg c ∑ x^3 = ∑lg x lg y; lg∑ x^2+ lg∑ x^3+ lg∑ ^4 = ∑ х^2 lg y
lgy = a+ bx	an + b ∑ = ∑lg y; a ∑ х + b ∑ x^2 = ∑ x lg y
y = а+ bx+ сх^2	na + b ∑ х + с ∑ х^2 = ∑ у а ∑ х + b ∑ x^2 + с ∑ х^3 = ∑ ху a ∑ x^2+ b ∑ x^3 + с ∑ x^4 = ∑ x^2у
у =аbx	n lg a+ lg b ∑ x = ∑lg y lg a ∑ x + lg b ∑ x^2 = ∑lg x lg y
y = a+b - lgx	an+ b ∑lg x = ∑ у a ∑lg х + b ∑(ln х) ^2= ∑l gx lg y

Рассмотрим второй случай — метод наименьших квадратов для
нелинейных форм. Пусть Y — целевая функция; у₁, у₂,..., у_n —
набор ее наблюдений; х₁, х₂,..., х_n — переменные факторы. Наблюдения 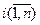представляют из себя вектор

X _i = (x _1i, x _2i,..., x_mi).

Необходимо целевую функцию Y выразить через вектор Х посредством функции f, вид которой известен, однако неизвестны
некоторые её параметры d₁, d₂,..., d_k. Тогда для Y _i можно записать

Y_i = f_i (d₁, d₂,..., d_k; x ₁, x ₂,..., x _mi) + F_i ,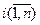

где F_i — отклонение (ошибка).

Если исключить параметры d₁, d₂,..., d_k то функция запишется
в виде

Y _i = f _i(х„.,х„,,х„„.) + F _i,

куда входят параметры, которые необходимо найти МНК.

Минимизируя

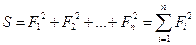
и используя метод Маркварда, введем векторы

; ; ; ,

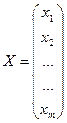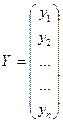сформируем задачу в виде: найти такое Х *, что при F = Y — f целевая
функция (сумма квадратов остатков) S = F^TF минимизируется.

Приближенное значение Х_i, получаемое на t -том шаге итеративного процесса, и последующее приближенное значение Х _t+1 связаны
между собой вектором поправки ∆ Х, т.е.

Формула вектора поправки ∆Х согласно условию минимизации, выводится из решения системы линейных уравнений

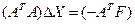откуда 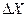= -(А ^T А)^-1 A ^т F,

где А — первая частная производная от F, определяемая как матрица Якоби
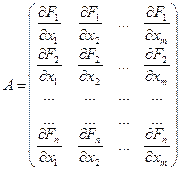при x = x_t

Это формулы итерации по методу Ньютона — Гаусса. При их
использовании, если степень нелинейности f (х) высока, а стартовое
значение х далеко отстоит от минимизирующего значения, то велика вероятность «раскачки» 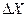и расходимости итеративного процесса.

Левенберг и Марквардт в процедуре Ньютона — Гаусса предложили искать корректирующий вектор ∆ Х из уравнения

(A ^т A + v ² I) ∆ Х = - А ^т F;

где I — единичная матрица, а v— некоторая величина, называемая числом Марквардта. Тогда

∆ Х = -(A ^т А + v ² I)^-1 А ^т F.

При v = 0 приходим к формуле ∆ Х = -(A ^т А + v ² I)^-1 А ^т F. При вычислениях рекомендуется за начальное значение принимать v =0,001,
затем на каждом шаге увеличивать v в десять раз, до тех пор, пока S
не начнет уменьшаться.

Дата добавления: 2015-04-24