Построение и анализ экологических моделей. Регрессионный анализ

Лекция 5.

При построении математических зависимостей могут быть две
формы связей между функцией и переменными: функциональная и
регрессионная. Если функциональные связи точно выражаются аналитическими уравнениями, то регрессионные связи выражаются уравнениями лишь приближенно. В общем случае можно сказать, что связь
между функцией и аргументами будет тогда функциональной, когда
будут учтены все аргументы, определяющие значения функции.

Уравнение регрессии составляется исследователем на основе характера связи между функцией и аргументами. Вопрос о форме связи решается, как правило, поэтапно.

Вначале рассматривается линейная форма связи вида:

Y = b₀ + b ₁ X ₁ +b ₂ X ₂ +...+ b_n X _n

где Х_i — факторы (i = 1, 2,..., n), так как такая форма связи часто встреча-

ется на практике и для нее разработан хороший математический математический аппарат.

При этом могут решаться следующие задачи:

• установление точности определения коэффициентов уравнения регрессии b _i в виде значений дисперсии S ² (b _i) или величины доверительных интервалов;

• установление значимости коэффициента b_i;

• проверка адекватности установленной формы связи и экспериментальных данных.

При установлении тесноты связи между Y и Х решается задача
установления строгости соблюдения функциональной зависимости
между изменениями Y и Х. Для оценки тесноты связи между случайными переменными величинами используются показатели:

а) в случае линейной формы связи

• коэффициент парной корреляции r_yx или r_xy, характеризующий строгость соблюдения пропорциональности, т.е. близость ис-
следуемой формы связи с линейной;

• коэффициент частной корреляции , характеризующий
тесноту связи между изучаемыми переменными при условии, что
влияние остальных факторов исключается;

• коэффициент множественной корреляции 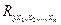, характеризующий суммарное влияние всех факторов на величину Y;

б) в случае нелинейной формы связи

• корреляционное отношение р, которое является характеристи-
кой, насколько строго соблюдается функциональная связь между
исследуемыми переменными. Этот показатель применим и для оценки
тесноты связи в случае линейной формы связи. В этом случае он
равен абсолютному значению коэффициента парной корреляции;

• множественное корреляционное отношение 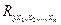, которое
является характеристикой тесноты связи между Y и Х. Аппарат корреляционно-регрессионного анализа используется в двух направлениях:

1) для проведения статистического анализа результатов наблюдений пассивных экспериментов, в которых независимые переменные Х. не могут изменяться экспериментатором, т.е. не регулируются. В результате такого анализа решение вопроса о виде формы связи
не является окончательным, т.е. можно принять в качестве математической модели процесса большое число уравнений регрессии, которые могут удовлетворять полученным экспериментальным данным;

2) совместно с методом наименьших квадратов для планирования статистических экспериментов и анализа их результатов. В этом
случае планирование экспериментов осуществляется в соответствии
с принятым видом уравнения связи Y и Х.

В соответствии с числом учитываемых независимых переменных
Х _i и характером связи между Y и Х различают:

а) по количеству исследуемых переменных

• парный корреляционно-регрессионный анализ;

• множественный корреляционно-регрессионный анализ;

б) в зависимости от формы связи

• линейный корреляционно-регрессионный анализ;

• нелинейный корреляционно-регрессионный анализ.

Метод наименьших квадратов. Широкое распространение в практике математического моделирования получили уравнения регрессии вида:

у = f (х),

где х — величина, которая рассматривается как случайная независимая переменная;

у — случайная зависимая величина. При линейной форме связи
эту зависимость можно выразить уравнением прямой:

Y = b ₀ + b ₁ Х,

для построения, которого требуется проведение экспериментов в объеме n, в каждом из которых должна фиксироваться пара значений (х _i; у _i). Результаты эксперимента представляются либо в виде таблицы (табл. 5.1), либо в виде графиков (рис. 5.1).

Таблица 5.1

Значение фактора Х i	Х 1	Х 2	...	Х i	...	Х n
Значение функции Y i	Y 1	Y 2	...	Y i	...	Y n

Дата добавления: 2015-04-24