Представление результатов эксперимента

Рассматривая экспериментальные точки (х _i; у _i) в прямоугольной системе

Рис. 5.1. График результатов эксперимента

координат, мы видим, что в случае рис. 5.1. а) часть
точек лежит на прямой Y = b ₀+ b ₁ Х, часть ниже и выше ее. В этом
случае для построения модели зависимости Y от Х можно использовать линейное уравнение регрессии. В случае рис. 5.1. б) — нелинейное уравнение, а в случае рис. 5.1. в) применение регрессионного анализа проблематично.

Рассмотрим случай а), здесь через совокупность точек проведена прямая

Y = b ₀+ b ₁ Х которая показывает на существование зависимости между Х и Y и наша задача состоит в том, чтобы определить
коэффициенты b ₀и b ₁ определяющие положение прямой относительно всех и экспериментальных точек таким образом, чтобы сумма квадратов отклонений между значениями у _i, полученными при
эксперименте и значениями у при х _i, подставленное в предлагаемое
(гипотетическое) уравнение, было минимальным. Для этого используется метод наименьших квадратов (MHK).

Пусть разность между экспериментальным у _i и гипотетическим
значениями у равна при х _iδ = у _i - у, или δ = у _i - (b ₀ +b ₁Х). При изменении величин b ₀и b ₁меняется, и δ. Возьмем функцию

являющуюся функцией двух переменных b ₀и b ₁. Наилучшая пря-
мая, описывающая зависимость Y от Х для экспериментальных данных будет такая, где значение

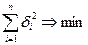
Для нахождения минимума возьмём частные производные от
S (b ₀, b ₁) и приравняем их к нулю.

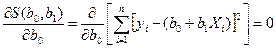
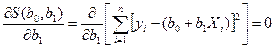
Решая эту систему, называемую системой нормальных уравнении МНК, получим:

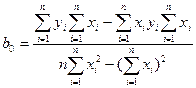
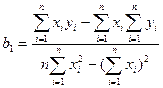
Коэффициент b ₀ — есть постоянная уравнения, которая определяется при

х = 0, а b ₁ — угол наклона прямой регрессии Y к оси 0Х

В качестве меры зависимости между случайными величинами
используется коэффициент корреляции, определяемый по формуле

Коэффициент корреляции всегда находится в пределах — 1< r <+1. Если случайные величины Х и Y независимы, то r = 0; если связь между Х и У функциональная, то r = 1. В качестве меры адекватности регрессионной модели статистическим данным часто используют коэффициент детерминации

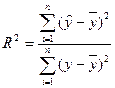
Где 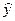— расчетное значение (теоретическое по полученному уравнению

регрессии 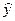= b _o + b ₁ х, где знак «ˆ» над у обозначает, что уравнение по-
лучено по МНК для величины Y от Х _i,

где 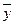— среднее значение у

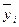— значения у в i -том опыте (i =1, 2,..., n).

Чем больше значения R ², тем выше степень адекватности уравнения регрессии опытным данным.

Для уравнения регрессии вида

у =bo+b ₁ х ₁ +b ₂ х ₂ +…+b _i х _i +…+b _m х _m;

многих переменных х,, х,..., х„, результаты i го опыта записываются в виде

у =b _o x _0i +b ₁ х _1i +b ₂ х _2i +…+b _m х _mi;

где x _0i= 1 при всех i =1,n,.

n — общее число опытов в эксперименте.

Для определения коэффициентов уравнения регрессии b ₀, b ₁,
b ₂, ...,,b _m, может быть использован МНК, который минимизирует
сумму квадратов регрессионных опытов

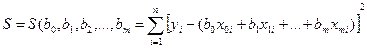
Если представить результаты эксперимента в матричной форме
Y = ХВ,

где ; ; .

то можно записать S = (Y — XB)^T(Y — XB) (индекс «т» означает транспонирование).

Исходя из условий минимизации , откуда (X ^T X) B = X ^T Y.

Следовательно, оценка МНКесть такая, при которой коэффи-
циенты уравнения регрессии равны В = (X^TX)^-1 Х^TУ (индекс "-1"
означает обратную матрицу). Коэффициент детерминации (скорректированный) равен:

Оценка меры автокорреляции случайной величины,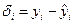
как правило, производится с помощью статистики Дарбина-Уот-
сона

При значении D (δ), близком к двум, говорят, что автокорреляция отсутствует (что желательно).

Пример. Врезультате эксперимента зафиксированы пары значений (х_i,у_i), приведенных в табл. 5.2: Построить уравнение регрессии вида у = b ₀+b₁ х

Таблица 5.2

Дата добавления: 2015-04-24