Статистические оценки гипотез об экологических моделях

Точечные оценки параметров распределения случайных величин. Основными методами получения точечных оценок являются метод моментов, метод наименьших квадратов (МНК) и метод максимально- го правдоподобия (ММП).

Метод моментов является наиболее простым и общим способом
точечной оценки. Пусть имеется выборка (х₁, х₂,..., х_n) случайной
величины Х. Среднее значение наблюдаемого признака можно оп-
ределить по формуле

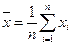
Таким образом, представляет собой эмпирическое, или выборочное среднее. Если вычислено среднее, то легко найти отклонение каждого наблюдения δ, от среднего δ_i = х _i — .

Величину S ² = 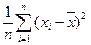называют дисперсией или вторым центральным моментом эмпирического распределения

m ₂ = S ²

В случае одномерного эмпирического распределения произволь-
ным моментом порядка К называется сумма К-тых степеней отклоне-
ний результатов наблюдений от произвольного числа С, деленная
на объем выборки n

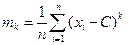
где k может принимать любые значения натурального ряда чисел.
Начальным моментом первого порядка является выборочное среднее , т.е.

что мы видели ранее. Если С = , то имеем центральные моменты

…………………

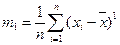
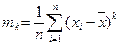
Среднеквадратическое отклонение равно

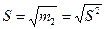
Выборочное значение коэффициента вариации V, являющееся
мерой относительной изменчивости наблюдаемой случайной вели-
чины, вычисляют по формуле

или в процентах

Если известна форма связи искомого параметра с моментами, то
вначале находят выборочные оценки моментов, а затем, используя
форму связи, вычисляют оценку самого параметра. Например, в
качестве меры симметричности графика распределения случайных
величин, используется коэффициент асимметрии А_s который для симметричного распределения равен нулю. Для оценки асимметричности используется формула

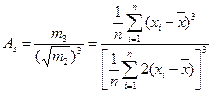
Если А_s > 0, то график плотности вероятности имеет «скос» с
левой стороны от 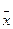, а если А_s < 0, то — с правой.

В качестве меры «крутости» графиков распределения случайных
величин используют коэффициент эксцесса E_k, характеризующий
«крутость» графика по сравнению с кривой Гаусса. Для оценки Е,
используется формула

Если E_k ≥ 0, то кривая островершинная, при E_k < 0 — плоско-
вершинная (пологая). Метод моментов, как правило, приводит к
состоятельным оценкам. Однако при малых выборках оценки мо-
гут оказаться значительно смещенными и малоэффективными. Метод моментов достаточно эффективен для оценки параметров нормально распределенных случайных величин.

Метод наименьших квадратов в основном используется для оценки коэффициентов уравнения регрессии, например в ального параметра используется процентная частота, то ее ошибка вычисляется по формуле

и будет рассмотрен в регрессионном анализе.

Метод максимального правдоподобия имеет большое преимущество по сравнению с другими методами точечной оценки. Он
дает состоятельные, распределенные асимптотически нормально, эффективные оценки. Хотя эти оценки могут быть несколько смещенными.

Метод состоит в следующем. Пусть имеется выборка (х ₁, х ₂,..., х_n),
а рассматриваемый признак х имеет распределение плотности веро-
ятностей f(x, Θ), где Θ есть неизвестный параметр, который требу-
ется оценить по выборке. В силу случайности попадания в выборку величины х _i. вероятность осуществления данной выборки равна произведению плотности вероятностей

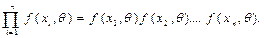
Такая функция называется функцией правдоподобия выборки и обозначается через L, т.е.

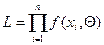
Выборочная оценка, которая обращает в максимум функцию правдоподобия, называется оценкой максимума правдоподобия.

Для нахождения максимума определяем частную производную
и приравниваем ее к нулю,

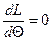
Например, для показательного распределения f(x, Θ)= Θе^Θx,
где Θ — неизвестный параметр, который следует оценить по выборке
(x₁,х₂,...,х_n), составим функцию правдоподобия

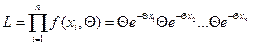
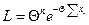
Прологарифмируем функцию L

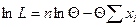
Теперь ее продифференцируем и приравняем к нулю

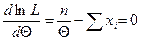
Отсюда

Для оценки величины рассеивания средних выборочных относительно математического ожидания генеральной совокупности в
случае нормального распределения случайной величины х можно
применить формулу

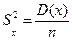
где
D(x) — известная дисперсия генеральной совокупности;

n — объем выборки.

Средняя ошибка выборочной средней

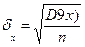
Несмещенная оценка дисперсии, получается, по методу максимального подобия с поправкой

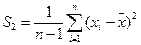
Характеристика рассеивания дисперсии S определяется по формуле

Средняя ошибка выборочной дисперсии

Для нормального распределения

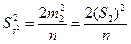
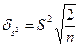
При обработке статистических данных используют следующие виды оценок:

1. Средняя арифметическая для объема выборки n

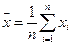
При разделении выборки на k групп, в которых x_j встречается m_j раз

Средняя арифметическая в группе k

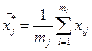
Средняя групповая

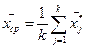
4.2. Средняя геометрическая используется тогда, когда вариант х _i
имеет размерность нулевого порядка. Величины такой размерности
выражают вторичные признаки, являющиеся отношением двух одноименных величин, например измеренная в результате опыта величина сравнивается с некоторым стандартным значением. В результате получается, что величина х _iявляется безразмерной. Тогда
средняя геометрическая равна

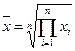
или

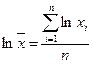
4.3. Средняя гармоническая имеет свойство усреднять при неизменной сумме величин, обратных усредняемым. Она применяется
тогда, когда варианта х _iпредставлена обратной величиной и определяется по формуле

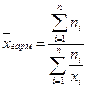
4.4. Средняя квадратическая используется тогда, когда варианта
представляет размерность второго порядка, например, когда х _iесть
площадь поверхности, полученная измерением длин сторон прямо-
угольника. В этом случае используется формула

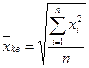
5.5. Медиана делит ранжированный ряд распределения вариант х _i на две равные части. Таким образом, в ранжированном ряду распределения
одна половина ряда имеет значения признака, превышающие медиану,
а другая — меньше медианы. Медиана является характеристикой центральной тенденции признака, особенно когда концы распределения расплывчаты и неясны.

5.6. Мода показывает значение величины х _i, имеющей наибольшую частоту в статическом ряду распределения. Так, в табл. 3.1 и на
рис. 3.1 показано, что мода равна хт = 1 при частоте т _i = 10.

4.7. Выборочная дисперсия

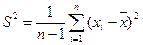
Среднее квадратическое отклонение .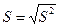

4.8. Дисперсия альтернативного признака используется тогда, когда признак измеряется двумя альтернативными значениями, например 0 и 1, да и нет, присутствует или не присутствует. Доля элементов выборки, обладающих признаком 1, равна .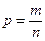

признаком 0

Средняя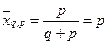

Дисперсия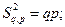

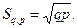
Интервальные оценки параметров распределения случайных вели-
чин. Точечные оценки параметров не дают информации о степени
близости оценки Θ_b к соответствующему теоретическому параметру

Θ. Поэтому более информативный способ оценки неизвестных пара-
метров состоит не в определении единичного точечного значения, а в
построении интервала, в котором с заданной степенью достоверности
окажется оцениваемый параметр, т.е. в построении так называемой
интервальной оценки параметра Θ.

Интервальной оценкой параметра Θ называется интервал, границы которого Θ_b1 и Θ_b2 являются функциями выборочных значений х ₁, х ₂, ... х_n и который с заданной вероятностью 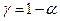накрывает оцениваемый параметр Θ

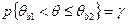
где α - уровень значимости.

Интервал (Θ_b1, Θ_b2) называется доверительным, его границы Θ_b1

иΘ_b1 являющиеся случайными величинами, соответственно нижним и верхним доверительными пределами. Любая интервальная оценка
может быть охарактеризована совокупностью двух чисел: шириной
доверительного интервала Н = Θ_b1 - Θ_b2, являющейся мерой точности оценивания параметра Θ, и доверительной вероятностью у, характеризующей степень достоверности (надежности) результатов,
Чаще всего в расчетах используется величина у равная 0,9; 0,95 и
реже 0,8; 0,85; 0,99; 0,999.

Общая процедура получения интервальной оценки состоит в
следующем:

1. Записывают определенное вероятное утверждение вида

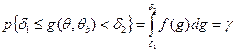
где f (g) — функция распределения плотности вероятностей случайной
величины g. Приэтом значения δ ₁ и δ ₂ определяют обычно с учетом дополнительных условий

2. Аргумент g преобразуют так, чтобы в окончательном виде
оцениваемый параметр оказался заключенным между величинами,
определяемыми по выборке. Это и будут границы доверительного
интервала (Θ_b1, Θ_b2). Функцию g(Θ, Θ_b2) выбирают таким образом,
чтобы она допускала подобное преобразование и имела известную
(лучше табулированную) функцию плотности вероятностей f (g). Последнее обстоятельство существенно упрощает определение значений
δ ₁ и δ ₂.

В качестве примера получим интервальную оценку математи-
ческого ожидания М(х) нормальной генеральной совокупности с
известной дисперсией D(x). Известно, что функция

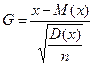
подчиняется нормированному нормальному распределению

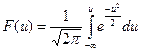
(см. приложение 1). Тогда можно записать:

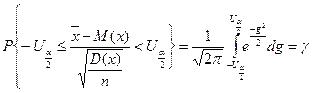
После преобразования аргумента получим:

Следовательно, для данного случая:

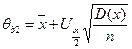
а ширина доверительного интервала

Для нормально распределенной случайной величины доверительный интервал определяется по формулам:

• если теоретическое значение дисперсии неизвестно, то для
математического ожидания доверительный интервал будет иметь вид:

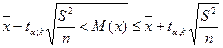
где k — число степеней свободы, k = n - 1;

t_a,k — табличное значение критерия Стьюдента, определяемое по таблице, приведенной в приложении 2;

• для теоретической дисперсии

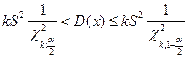
где k = n – 1, χ ²_{k;α /2}, χ ²_{k;1-α /2} - нижнее и верхнее значения критерия

Пирсона при заданных k и α/2, определяемое по таблице, приведенной в приложении 3.

Используя интервальные оценки, можно определить объем выборки, задаваясь точностью оценки. Если оценивается математическое ожидание, то точность оценки будет равна

При заданном значении δ и D(x) объем испытаний будет равен

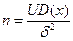
При неизвестном D(x) объем испытаний определяется по фор-
муле

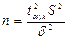
Если оценивать дисперсию D(x), то, задаваясь значением δ_g,
можно использовать уравнение

затем с помощью таблиц χ ² распределения (см. приложение 3) подо-
брать такое соотношение в левой части неравенства, чтобы оно удовлетворяло правую часть, и затем определить объем испытаний n = k+L.

Доверительный интервал для генеральной доли P устанавливается по формуле

где P_b — выборочная доля;

U_a/2 — критерий, выбираемый по таблице (см. приложение 4,
при U_a/2= x).

Величина U_a/2, вычисляется по формуле

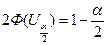
Откуда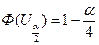

где S _pf – ошибка выборочной доли.

Если вместо доли в качестве оценки генерального параметра используется процентная частота, то ее ошибка вычисляется по формуле

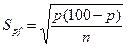
Границы доверительного интервала p+UpS ~ для генеральной доли устанавливаются с достаточной точностью в тех случаях, когда выборочные доли равны или не сильно отклоняются от
50% численности групп. Если же выборочные доли не равны
(75% < р < 25%) и тем более близки к нулю и единице, довери-
тельные границы для генеральной доли следует определять с по-
мощью вспомогательной величины < р,

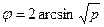
Эта величина, предложенная Р.Фишером, имеет распределение, близкое к нормальному. Ее параметром служит выборочная ошибка, равная .

Значения φ зависят только от р.

Для практического использования этой величины служит таблица, приведенная в приложении 5, в которой содержатся значения
φ для разных значений доли р, выраженной в процентах.

Пример. Из общего числа 5800 чел., проживающих в населен-
ном пункте, методом случайного отбора обследовано 1500 лиц, среди которых обнаружено 200 больных.

Доля больных

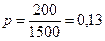или 13%

Ошибка доли

или 8%

Для доверительной вероятности γ =0,9 величина U_α/2=1,96=2.
Тогда доверительный интервал

Отсюда с вероятностью 0,90 следует заключить, что генеральная доля находится между Р_верх. = 0,15 и Р_ниж. = 0,11. Так как генеральная доля меньше 25%, исправим доверительный интервал с по-
мощью величины rp. Для доли больных

для Р %=13,0025 величина φ > 0,738 (см. приложение 5). Определим S _pf

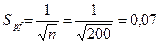
Отсюда границы для доверительного интервала р равны:

· нижняя 0,738 — 2 х 0,07 = 0,601;

· верхняя 0,738+ 2 х0,07 = 0 875.

Переводим значения р в исходные величины по таблице (см.
приложение 5): = 8,8% и =18,0%. Это значит, что с вероятностью
Р = 0,90 можно утверждать, что доля больных в населенном пункте
при данных условиях не должна выйти за пределы 8,8% — 18% от
общего числа жителей.

Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений,
симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рас-
сматриваться как гипотезы, которые необходимо проверить. Понятие «статистическая гипотеза» — более узкое, чем общее
понятие «научная гипотеза». Статистические гипотезы охватывают
поведение наблюдаемых случайных величин.

Статистическая гипотеза, являющаяся утверждением о значениях параметров конкретного вероятного распределения некоторой случайной величины (например, о средней дисперсии) называется параметрической.

Статистическая гипотеза является:

а) утверждением о некоторых свойствах вероятности распределений исследуемых случайных величин, (например, симметричности распределения, совпадения функций распределения двух и более случайных величин, принадлежности выборки к данному классу
вероятностного распределения);

б) независимым от вида вероятности распределения утверждением о параметрах случайных величин, например, равенстве
двух или более средних арифметических или дисперсии (при неизвестных вероятностных распределениях этих случайных вели-
чин), относится к параметрическим гипотезам. Проверка статистических гипотез осуществляется с помощью статистических критериев.

Выдвигаемая гипотеза, которую необходимо проверить, называется нулевой и обозначается H ₀. Гипотеза, которая противопоставляется нулевой, называется альтернативной и обозначается Н ₁.
Выделение нулевой гипотезы состоит в том, что H ₀, обычно рассматривается как утверждение, которое более важно, если оно отвергнуто. Это основано на общем принципе, согласно которому
теория должна быть отвергнута, если есть противоречащий пример, но не обязательно должна быть принята, если такого примера
найти нельзя.

Если конкурирующие гипотезы H ₀и H ₁полностью определяют распределение случайной величины х, например значение пара-
метра Θравным Θ (H ₀ ) или Θ (H ₁ ), соответственно такие гипотезы
называются простыми.

Гипотезы называются сложными, если они не полностью определяют параметры распределения. Например, если согласно некото-
рой гипотезе случайная величина распределена по нормальному за-
кону со средней М (х) и неизвестной дисперсией D(x), то в этом
случае будем иметь дело со сложной гипотезой. Гипотеза H ₁ альтернативная H ₀ тоже может быть сложной. Например, если по ги-
потезе H ₁случайная величина распределена по нормальному закону
с известной D(x) и средней М₁(х) > М₀(х) или М₁(х)≠М₀(х), то
очевидно, что гипотеза H ₁, не определяет полностью распределение,
поэтому ее следует считать сложной.

Таким образом, если распределение имеет всего k параметров,
часть которых неизвестна, то гипотеза также называется сложной.

Необходимо получить критерий, с помощью которого по наблюдаемому значению х можно сделать разумный выбор между
нулевой и альтернативной гипотезами. Построение критерия начинается с выбора такого множества на действительной прямой
(или в n -мерном пространстве), что если случайная величина примет
значение из этого множества, то принимается нулевая гипотеза
(H ₁ отвергается). Такое множество называют множеством принятия гипотезы (W₀). Дополнительное множество к множеству W₀ называется множеством отклонения гипотезы H ₀ (W₀), иликритическим множеством.

При проверке гипотезы H ₀против H ₁возможны два рода ошибок. Ошибки первого рода — это ошибка, когда принимается неверная гипотеза H ₀. Вероятность ошибки первого рода принято обозначать α, она называется уровнем значимости критерия. Обычно α
выбирают равным: 0,10; 0,05; 0,025 и 0,01.

Вероятность ошибки второго рода обозначают β. Вероятность
дополнительного события, т.е. правильного отклонения гипотезы H ₀ называется мощностью критерия. Следовательно, мощность критерия (W_кр) равна вероятности того, что наблюдение попадает в критическую область, если оно имеет альтернативное распределение, т.е. W_кр = 1 - β.

Процедура применения статистического критерия следующая.

1. Выдвигаются гипотезы H ₀и H ₁и задается уровень значимости α. На выбор уровня значимости может влиять отношение
исследователя к гипотезе до проведения эксперимента. Если есть
уверенность в истинности гипотезы, то необходимы убедительные свидетельства, чтобы отказаться от этой уверенности. В таких условиях нужны критерии высокого уровня и α выбирается
очень малой, чтобы попадание в критическую область было
крайне неправдоподобным, если верна гипотеза H ₀.

2. Выбирается статистический критерий проверки H ₀при уровне значимости αскритерием связана статистика критерия
Г=Г(х₁, х₂,..., х_n), которая является выборочной функцией с известн-
ным вероятностным распределением F (γ). Критическая область W
находится как подмножество выборочного пространства х, такое,
что вероятность

Р(Г W| H ₀) ≥ α.

В зависимости от альтернативной гипотезы

а) H ₁: Θ_b < Θ;

б) H ₁: Θ_b > Θ;

в) H ₁: Θ_b≠ Θ,

критическая область выражается через значения статистики Г и принимает одну из форм:

а) Г≤ Г₀;

б) Г≥Г_и;

в) Г≤Г_а или Г≥Г_в,

где Г₀, Г_и, Г_а, Г_в - квантили известного распределения, выбранные так, что при выполнении H ₀справедливо одно из соотношений:

а) Р_r(Г ≤ Г₀) = α ;

б) Р_r(Г ≥Г_и) = α;

в) Р_r(Г ≤Г_а) или Р_r(Г ≥ Г_в) = α /2.

Случаи а) и б) представляют односторонние критические области, а случай в) - двустороннюю критическую область;
Р_r - вероятность принятия гипотезы.

С критической областью W для данного критерия при уровне
значимости α однозначно связан доверительный интервал, которому соответствует вероятность

Р(Г W| Н₀) ≥1 — α ..

3. Если вычисленная по выборке статистика Г имеет значение

Г = Г(х₁, х₂ ,..., х_n),

которое не принадлежит W то гипотеза Н ₀принимается, в противном случае она отвергается и принимается гипотеза Н ₁. Возможен и другой подход. Пусть Г - вычисленное значение
статистики по выборке. Вычислим вероятность Р_a попадания Г в
критическую область. Эта вероятность называется фактически достигнутым уровнем значимости. Значение Р дает возможность при-
нимать или отвергать гипотезу при любом заранее заданном уровне
значимости а путем простого сравнения Р_a с α. Если Р_a меньше α,
то гипотеза Н₀ отвергается с уровнем значимости α, в противном
случае Н₀ принимается.

Дата добавления: 2015-04-24