Статистический ряд по интервалам

Зависимость числа интервалов от объема выборки

n	До 50	50 — 100	100 — 500	500 — 1000	Свыше 1000
k	6 — 8	8-10	10-13	13-15	15-20

При этом желательно, чтобы в каждом интервале было не менее
восьми наблюдений (в крайних интервалах число наблюдений может быть меньше восьми).

Для нашего примера принимаем k = 8. Определяем ширину
интервала (h) по формуле

h = 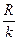= = 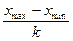15,8/8= 1,975

Принимаем h = 2,0, условно считаем Х _max = 16,0. Записываем
статистический ряд по интервалам (табл. 3.3). Эмпирической функцией распределения F _n(х) называют функцию накопленных (кумулятивных) частостей, для нашего примера
она имеет вид
Рис. 3.3.

Функция F _n(х) может быть изображена графически (см. рис. 3.3) в
координатах (х, F _n(х)). Функция F _n(х) служит оценкой неизвестной функции распре-
деления F (x) для случайной величины х.

Таблица 3.3

Номер интер- вала i	Интервал значений для х i.	Среднее значение х в ин- тервале, х i^*.	Частота наблюде- ний в интервале, mi.	Частость, wi	Накоп- ленная частость, wn,i
	0 ≤ х1 ≤ 2			0,09375	0,09375
	2 ≤ х2 ≤ 4			0,12500	0,21875
	4 ≤ x3 ≤ 6			0,15625	0,37500
	6 ≤ х4 ≤ 8			0,18750	0,56250
	8 ≤ x5 ≤ 10			0,15625	0,71875
	10 ≤ х6 ≤12			0,12500	0,84375
	12 ≤ х7 ≤ 14			0,09375	0,93750
	14 ≤ х8 ≤ 16			0,06250	1,00000
Сумма		1,00000	1,00000

Можно получить выборочную функцию распределения плотности вероятностей f_n (х) в сере-
дине интервалов х _i^* (см. ниже рис. 2.3)

f_n (х _i^*)= m_i /nh,

Рис. 3.3. Эмпирическая функция распределения нитратов в огурцах.

Например, для первого интервала

f_n (x _i ^*) = = 0,046875

Тогда f '_n(х) для нашего примера будет иметь следующий вид:

⌠ 0,00000 при х < 0

│ 0,04687 при 0 < x₁ < 2

│ 0,06250 при 2 < х₂ < 4

│ 0,07823 при 4 < х₃ < 6 130

f_n (x) = { 0,09375 при 6 < х₄ < 8

│ 0,07812 при 8 < х₅ <10

│ 0,06250 при 10 < х₆ < 12

│ 0,04687 при 12 < х₇ <14

⌡ 0,03125 при 14 < х₈ <16

Если генеральная совокупность N обладает двумерным признаком Х и Y, где Х и Y представляют собой случайные зависимые величины, то статистический ряд может иметь вид, приведенный:

в табл. 2.4 (когда обе величины Х и Y непрерывны);
табл. 2.5 (Х непрерывна, а Y дискретна);
табл. 2.6 (обе Х и Y дискретны).

В табл. (2.4 - 2.6) частота наблюдений m _ij показывает, сколько
встречается в опыте пар (х _i, у _j).

Таблица 3.4

Статистический ряд при непрерывных величинах Х и Y

Х   Y	Границы интервала
0,1<у1<2	0,2<у2<0,3	0,3<у3<0,4	0,4<у4<0,5
Грани- цы интер- вала	0 ≤ х1< 1,1	m 11= 5	m 12 = 4	m 13= 3	m 14= 1
1,1≤х2< 2,2	m 21= 1	m 22= 7	m 23= 6	m 24= 4
2,2 ≤x3<3,3	m 31 = 0	m 32 = 8	m 33= 5	m 34 = 2
2,2 ≤x3<3,3	m 41= 2	m 42= 4	m 43= 1	m 44= 3

Таблица 3.5

Статистический ряд, когда Х непрерывна, а Y дискретна

YX	Значение у,.
y1= 2	y2 = 4	y3 = 6	y4 = 8
Грани- цы интер- вала	0,5≤ х 2<1,5	m 11= 4	m 12=6	m 13=4	m 14= 2
1,5≤ х 2<2,5	m 21= 3	m 22=5	m 23=6	m 24=5
2,5≤ х 2<3,5	m 31= 1	m 32= 5	m 33=4	m 34=7

Таблица 3.6

Статистический ряд, когда Х и Y дискретны

У Х	Значение у,.
	.10	m»= 5	т,,=4	m»= 8	т — 7	т =2 1з
Значе-		т,,=2	изб	и,,=4	т4= 3	и,,= 2
ние х,.		т =1 зз	т,,=6	m»= 5	и =1 з~	тзз 2
		m4) 3	т =3 42	т,,=4	т =5 44	т,,=6

Если генеральная совокупность N обладает р-мерным признаком

(L = l, 2,...,1,..., р), где
x₁, x₂, x₃, …, x_n, …, х_p — случайные величины, то статистический ряд будет состоять при выборке n из n векторов

(x₁₁, x₂₁, x₃₁, …, x_n1)

(x₁₂, x₂₂, x₃₂, …, x_n2)

…………………….

(x_1n, x_2n, x_3n, …, x_nm)

где х _ij — случайная величина х_j в i -ом испытании (наблюдении).

Результаты наблюдений могут быть также представлены в виде
матрицы

X =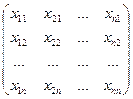

назад

Дата добавления: 2015-04-24