Статистические оценки параметров распределения случайных величин по выборкам

Лекция 4.

Основная задача выборочного метода заключается в том, что-
бы на основе изучения выборочной совокупности получить та-
кие выборочные характеристики, которые как можно более точно отражали бы характеристики генеральной совокупности.
Пусть изучается некоторый признак Θ. По результатам выборки определяется оценка этого признака Θ_b. Как бы тщательно ни была
организована выборка, будем иметь некоторую ошибку = | Θ_b — Θ|,
которая будет отличаться от нуля. С этой точки зрения основная
задача выборочного метода будет заключаться в том, чтобы величина была как можно меньше.

Чтобы выборочную оценку можно было считать, доброкачественной и пригодной для решения поставленных задач, она должна обладать определенными свойствами. Наилучшие оценки обладают такими свойствами, как несмещенность, состоятельность, эффективность и достаточность.

Выборочная оценка называется несмещенной, если ее математическое ожидание при любом объеме выборки равно значению пара-
метра в генеральной совокупности, т.е.

М(Θ_b) — Θ = 0.

Если же имеется смещение, т.е.

М(Θ_b) — Θ = β,

то величина β отражает это смещение.

Пусть исследуется признак Х в генеральной совокупности, из
которой сделана выборка х₁, х₂,..., х_n. Средняя арифметическая
выборочная

является оценкой генеральной средней M(x), так как

M(x)=M

Математическое ожидание выборочной средней равно средней
генеральной совокупности: M(x) = (x).

Выборочная оценка Θ_b параметра Θ, полученная на основе n
независимых наблюдений, называется состоятельной, если предел
вероятности

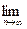P (Θ_b - Θ < ) =1.

Таким образом, разность |Θ_b – Θ| будет сколь угодно малой, а
предел стремится к единице при увеличении объема выборки при
>0. Свойство очевидно, так как чем ближе n к ∞, тем ближе
оценка Θ_b к Θ. Отсюда следует, что состоятельность оценки возрастает с увеличением объема выборки.

Выборочная несмещенная оценка называется эффективной, если
она имеет минимальную дисперсию по сравнению с другими возможными оценками. Так, например, имеются две выборочные оценки Θ_b1 и Θ_b2 с дисперсиями D(Θ_b1) > D(Θ_b2), тогда эффективной будет
оценка Θ_b2. Достаточной называют выборочную оценку, если она
включает всю информацию, которая содержится в выборке относительно определенного параметра. Если, например, по выборке
(х₁, х₂,..., х_n) производится оценка неизвестной вероятности Р, то вполне достаточно знать сумму варианта , т.е. общее число случаев, благоприятствующих данному событию. Отдельные же значения х_i уже не содержат никакой новой информации и ничего не
поясняют относительно значений Р. Выборочные оценки могут быть
точечными и интервальными.

Точечные оценки — это оценки некоторых неизвестных числовых параметров распределения случайных величин. Они представляют собой числа, полученные путем подстановки выборочных значений

х₁, х₂,..., х_n, в формулу для оценивания искомого параметра.
Точечные оценки параметров Θ _b не дают информации о степени
близости к соответствующему теоретическому параметру генеральной совокупности Θ. Поэтому более информативный способ оценивания неизвестных параметров состоит в построении интервала, в котором оказывается оцениваемый параметр.

Интервальной оценкой параметра Θ называется интервал, гра-
ницы которого Θ _b1 и Θ _b2 являются функциями выборочных значе-
ний х₁,х₂,...,х_n, и который с заданной вероятностью накрывает
оцениваемый параметр Θ

Р{ Θ _b1 < Θ < Θ _b2} = .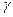

Величина 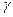называется доверительной вероятностью или надежностью, с которой оценка Θ заключается в интервал (Θ _b1 и Θ _b2), она
записывается в виде 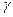= 1 - α, где α — уровень значимости, определяющий величину вероятности того, что оценка Θ выйдет за пределы интервала Θ _b1 и Θ _b2.

Ширина доверительного интервала равна Н = Θ _b1 - Θ _b2.

Дата добавления: 2015-04-24