
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения, приводящиеся к возвратным
|
|
|
|
Возвратные уравнения нечетной степени
Пример 3. Решить возвратное уравнение нечетной степени
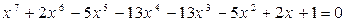 .
.
Решение
Такое уравнение (возвратное нечетной степени) всегда имеет корень 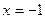 (попробуйте самостоятельно доказать это в общем виде) следовательно, по теореме Безу, его левая часть делится на x + 1.
(попробуйте самостоятельно доказать это в общем виде) следовательно, по теореме Безу, его левая часть делится на x + 1.
Выполним это деление по схеме Горнера:
| -5 | -13 | -13 | -5 | -1 | ||||
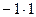
| 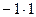
| 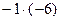
| 
| 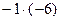
| 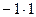
| 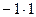
| ||
2 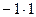 = 1 = 1
| -5 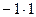 = -6 = -6
| -13 + 6 = -7 | -13 + 7 = -6 | -5 + 6 = 1 | 2 - 1 = 1 | 1 - 1 =0 |
В частном получим многочлен:  .
.
Уравнение примет вид: 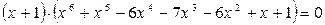 .
.
Осталось решить возвратное уравнение четной степени:
 .
.
Делим обе части на 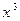 :
: 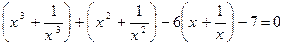 .
.
Снова полагаем 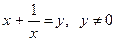 , нам уже известно, что тогда получим:
, нам уже известно, что тогда получим:
 .
.
Выразим 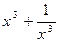 через y. Для этого возведём обе части равенства
через y. Для этого возведём обе части равенства 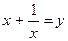 в куб, получим:
в куб, получим:
 .
.
Выполним подстановку и придём к уравнению  .
.
Решим его, раскладывая левую часть на множители:
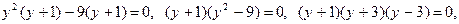
 .
.
Получаем три уравнения  .
.
Первое уравнение  не имеет действительных корней,
не имеет действительных корней,
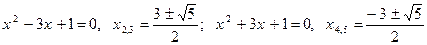 .
.
Ответ: 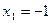 ,
,  .
.
Пример 4. Решите уравнение 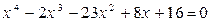 .
.
Решение
Это уравнение не является возвратным, но его можно легко привести к возвратному простой подстановкой, заменив x на 2u. Подставляя в уравнение x = 2u, получаем:
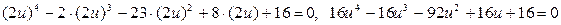 .
.
Полученное уравнение уже является возвратным, но его можно упростить, разделив обе части уравнения на 4, 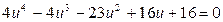 .
.
Делим обе части уравнения на 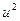 , а затем, делая подстановку
, а затем, делая подстановку  , находим:
, находим: 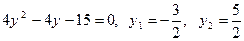 .
.

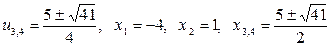 .
.
Ответ: 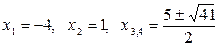 .
.
Пример 5. Решите уравнение, преобразуя его в возвратное
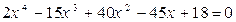 .
.
Решение
Чтобы свести уравнение к возвратному, необходимо сделать такую подстановку x = ku, где k - неопределенный коэффициент ( ), который предстоит найти.
), который предстоит найти.
Коэффициенты членов, равноотстоящих от концов многочлена должны быть равны. Коэффициент при первом члене: 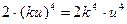 .
.
Коэффициент при этом члене должен быть равен по модулю 18, т. е. 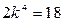 ,
, 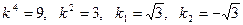 .
.
Теперь сделаем подстановку при  .
.
Уравнение примет вид: 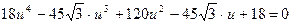 ,
,
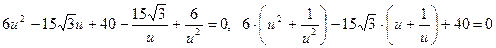 .
.
Положим 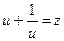 , тогда
, тогда 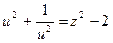 . После подстановки в уравнение получим
. После подстановки в уравнение получим 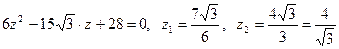 .
.
Подставляя вместо z значения, получим два квадратных уравнения
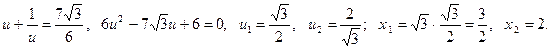
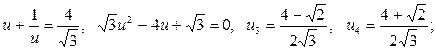
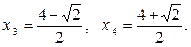
Если 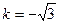 , тогда, при подстановке
, тогда, при подстановке  получим возвратное уравнение, которое решается теми же методами:
получим возвратное уравнение, которое решается теми же методами:
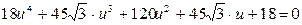 .
.
Ответ:  .
.
Задание 2
Решите уравнения.
1. 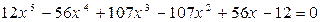 . 2.
. 2. 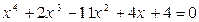 .
.
3. 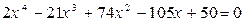 . 4.
. 4. 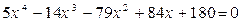 .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 847; Нарушение авторских прав?; Мы поможем в написании вашей работы!