Многочлены и их корни

Решение алгебраических уравнений выше второй степени

Упражнения

35. Доказать, что корни уравнения действительные (k, n и p - действительный числа). Найти условие, при котором корни этого уравнения будут равны между собой.

36. Доказать, что корни уравнения всегда действительные:

Указание. Преобразовать уравнение, найти дискриминант и преобразовать его к виду:

37. Доказать, что уравнение не может иметь действительных корней, если a, b, c не равны между собой.

38. При каком значении a один из корней уравнения будет квадратом другого?

39. Найти соотношение между коэффициентами уравнения если один корень вдвое больше другого.

40. При каком значении корни уравнения удовлетворяют соотношению (и - корни уравнения)?

41. При каком значении корни уравнения относятся как 3:2?

42. Уравнения и имеют общий корень. Найти зависимость между p и q.

43. При каких значениях k корни уравнения заключены между числами -6 и 1?

44. Для каких значений a, один из корней уравнения

больше 3, а другой меньше 2?

45. Найдите значения a, при которых оба корня уравнения

принадлежат отрезку

46. При каких значениях a корни уравнения лежат между корнями уравнения

47. Если один из корней уравнения равен обратному значению корня уравнения то Доказать.

48. Доказать, что корни уравнения обратны корням уравнения

49. Доказать, что если и - корни уравнения то

50. Составить квадратное уравнение, корни которого были бы равны сумме и произведению корней уравнения.

51. и - корни уравнения Не решая уравнение, составьте квадратное уравнение, корни которого были бы и

52. Дано уравнение, корни которого и; составить новое квадратное уравнение, корни которого были бы и

53. В уравнении определить a так, чтобы корни уравнения и были бы связаны соотношением

Решить уравнения на множестве действительных чисел.

54. 55. 56.

57. 58.

59. 60.

61.

Решите аналитически и графически уравнения.

62. 63. 64.

65. 66. 67.

68.

69. Найти все корни уравнения удовлетворяющее неравенству

70. Найдите все значения параметра a, при каждом из которых уравнение имеет три различных корня; найдите эти корни:

71. Найдите все значения параметра a, при каждом из которых уравнение имеет только один корень:

a) б)

Определение. Многочленом степени n от переменного x называется алгебраическое выражение вида

,

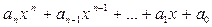где n - целое неотрицательное число, - любые действительные числа, причем .

Многочлен нулевой степени есть отличное от нуля действительное число. Будем также считать многочленом постоянную величину, равную нулю; такой многочлен будем называть нуль многочленом или просто нулём. В отличие от всех других многочленов нуль-многочлен не имеет степени.

Многочлены от переменного x будем обозначать символами P(x), Q(x), R(x), S(x) и т. д.

Числа будем называть коэффициентами многочлена. Коэффициент 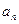называется старшим коэффициентом или коэффициентом при переменной наивысшей степени, а коэффициент 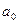- свободным членом.

Например коэффициентами многочлена 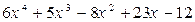являются числа 6, 5, -8, 23, -12. Среди них 6 - старший коэффициент, -12 - свободный член.

Одночлены 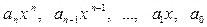называются членами многочлена.

Если какой-нибудь коэффициент равен нулю, то член с этим коэффициентом не пишут. Если коэффициент, отличный от 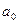, равен единице, то его также не пишут (коэффициент).

Например, многочлен 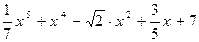имеет коэффициенты 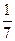, 1, 0, - 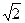, , 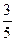7; многочлен 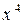имеет коэффициенты 1, 0, 0, 0, 0.

Многочлен считается известным, если известны все его коэффициенты и порядок их следования.

Дата добавления: 2015-04-24