
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Возвратные уравнения
Схема Горнера
Пусть дан многочлен  , который надо разделить на двучлен x - x0.
, который надо разделить на двучлен x - x0.
Для этого, коэффициенты данного многочлена запишем в верхней строке таблицы.
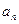
| 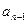
| ... | 
| 
| 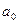
| 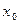
|

| ... | 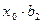
| 
| 
| ||

| 
| ... | 
| 
| остаток |
Во второй строке записывается произведение 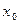 на предыдущие коэффициенты частного.
на предыдущие коэффициенты частного.
В третьей строке записываются коэффициенты частного и остаток.
Как получаются коэффициенты частного?
Обозначим коэффициенты частного: 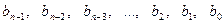 .
.
Нижние индексы у коэффициентов частного на единицу меньше, чем у делимого. И это понятно, потому что в частном получится многочлен степени на 1 меньшей, чем у делимого. Так, если у делимого наивысшая степень была 5 и был член, содержащий  , то в частном будет самая высокая степень 4 и старший коэффициент частного:
, то в частном будет самая высокая степень 4 и старший коэффициент частного:  .
.
Посмотрим, как это делается на примерах.
Пример 1. Найти частное и остаток от деления многочлена
 на x - 3.
на x - 3.
Решение
В верхней строке таблицы записываются коэффициенты данного многочлена в порядке убывания их индексов, а в правом уголке (можно в левом, дело вкуса) записывается число 3. Надо заметить, что члена, содержащего 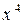 нет, значит, коэффициент при этом члене равен нулю - этот ноль записывается в таблицу. Об этом следует помнить.
нет, значит, коэффициент при этом члене равен нулю - этот ноль записывается в таблицу. Об этом следует помнить.
| -13 | -11 | -6 | ||||
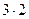
| 
| 
| 
| 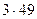
| ||
0 + 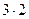 = 6 = 6
| -13 +  = 5 = 5
| 5 +  = 20 = 20
| -11 +  = 49 = 49
| -6+ 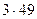 =141 =141
|
Получаем частное  ; остаток или значение многочлена в точке x = 3 равно P(3) = 141.
; остаток или значение многочлена в точке x = 3 равно P(3) = 141.
Ответ: частное  ; остаток или значение многочлена в точке x = 3 равно P(3) = 141.
; остаток или значение многочлена в точке x = 3 равно P(3) = 141.
Пример 2. Найти частное и остаток при делении  на x + 2.
на x + 2.
Решение
| -3 | - 2 | |||||
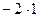
| 
| 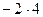
| 
| 
| ||
0 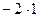 = -2 = -2
| 0  = 4 = 4
| -3 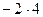 = -11 = -11
| 7  = 29 = 29
| 2 - 58 = -56 |
Ответ: частное: 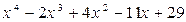 ; остаток: -56 (значение многочлена в точке -2).
; остаток: -56 (значение многочлена в точке -2).
Пример 3. Найти частное и остаток при делении  на
на 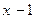 .
.
Решение
| -2 | -13 | ||||

| 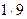
| 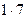
| 
| ||
7 +  = 9 = 9
| -2 + 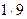 = 7 = 7
| -13 + 7 = -6 | 6 - 6 = 0 |
Ответ: частное:  ; остаток равен нулю, значит данный многочлен делится без остатка на x - 1.
; остаток равен нулю, значит данный многочлен делится без остатка на x - 1.
Задание
1. Найти частное и остаток при делении многочленов на двучлен, применяя схему Горнера:
а)  на x + 4; б)
на x + 4; б) 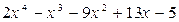 на x – 1
на x – 1
Определение. Уравнения вида
 , где
, где 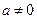 (1)
(1)
называются возвратными или симметричными.
Отличительной особенностью таких уравнений является равенство коэффициентов, равноотстоящих от его начала и конца.
Свойство 1. Возвратное уравнение не может иметь число 0 своим корнем. В самом деле, если допустить, что x = 0 - корень уравнения, тогда, при подстановке в уравнение, получим ложное равенство a = 0 (по определению 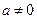 ).
).
Свойство 2. Если возвратное уравнение имеет своим корнем число a, то оно имеет и корень, равный 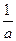 .
.
Доказательство
В самом деле, пусть x = a - корень возвратного уравнения
 , причём
, причём 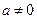 ,
,
тогда,  . (2)
. (2)
Подставим в левую часть данного уравнение значение  , получим:
, получим:
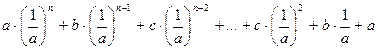 или
или
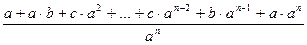 ,
,
но из равенства (2) следует, что  , причем
, причем 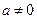 , следовательно,
, следовательно, 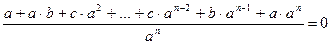 , а это и означает, что
, а это и означает, что 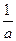 - корень данного возвратного уравнения (1).
- корень данного возвратного уравнения (1).
При решении возвратных уравнений часто применяется подстановка
 .
.
Пример 1. Решить уравнение на множестве действительных чисел
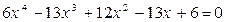 .
.
Решение
Это уравнение возвратное четной степени. Делим обе части уравнения на 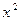 , тем более, что
, тем более, что 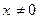 (следствие 1), получим уравнение:
(следствие 1), получим уравнение:
 ,
,  ,
,
 .
.
Пусть 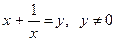 , тогда, возводя обе части этого равенства в квадрат, получим:
, тогда, возводя обе части этого равенства в квадрат, получим: 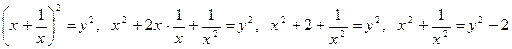 .
.
Подставляя новые переменные в уравнение, имеем:
 .
.
Значение 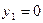 не удовлетворяет условию
не удовлетворяет условию  т является посторонним корнем. Остается одно значение:
т является посторонним корнем. Остается одно значение:  .
.
Делая обратную подстановку, получим 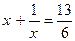 .
.
Отсюда находим  ,
, 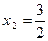 .
.
Ответ:  ,
, 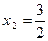 .
.
|
|
Дата добавления: 2015-04-24; Просмотров: 1269; Нарушение авторских прав?; Мы поможем в написании вашей работы!