Для любителей и знатоков. Решение уравнений повышенной трудности

Графическое решение

Аналитическое решение

Графическое решение

Для графического решения преобразуем уравнение:

Построим графики функций и

График функции будем строить в несколько этапов:

а) строим график функции

б) строим график функции "зеркально" отразив нижнюю часть кривой в оси OX;

в) строим график функции для этого достаточно график функции "опустить" вниз (осуществить параллельный перенос вдоль оси OY) на

г) полученный график полностью симметрично отразим в оси OX, "перевернем" вокруг оси OX на 180⁰.

В результате получим график функции.

График функции построим уже известным способом:

строим параболу и зеркально отражаем в оси OX только часть параболы, находящуюся ниже оси OX.

Находим абсциссы точек пересечения графиков, которые и будут являться решениями уравнения (см. рис. 43).

Рис. 43

Абсциссы точек пересечения следующие: 1,75; 2,5 и 3,25. Они и будут решениями уравнения.

Ответ:

Пример 24. Найти все корни уравнения удовлетворяющее неравенству Решить аналитически и графически.

Решение

Выясним, при каких значениях x квадратный трехчлен принимает положительные и отрицательные значения. Он имеет два корня:

и

Рис. 44

Таким образом, при и трехчлен положителен, а при трехчлен отрицателен (см. рис. 44).

Сразу заметим, что значения и не являются решениями данного уравнения, так как правая часть равна нулю, а левая часть не равна нулю.

Рассмотрим уравнение на промежутках, где квадратный трехчлен положителен и отрицателен.

Получим совокупность двух смешанных систем:

(1)

Рис. 45

Ясно, что система не имеет решений, т. е. ни один из корней уравнения (0 и 1) не входит в промежуток, который является общим решением первых двух неравенств (см. рис. 45).

Решим вторую систему (см. рис. 46):

(2)

Рис. 46

Система имеет единственное решение:

Ответ:

Строим графики функций и. Получим две точки пересечения, абсцисса только одной из них меньше, т. е. удовлетворяет условию задачи (см. рис. 47).

Рис. 47

Ответ:

Задание 5

Решите аналитически и графически уравнения:

1. 2. 3.

4. 5.

6. Найти все корни уравнения удовлетворяющее неравенству

Пример 25. Найти все значения параметра a, при каждом из которых уравнение имеет единственное решение.

Решение

Найдем решения для каждого значения a, а затем отберем те, которые удовлетворяют условию задачи, т. е. при которых уравнение имеет единственное решение.

Для каждого фиксированного a будем искать решения данного уравнения сначала на промежутке, а потом на промежутке, поскольку модуль обращается в нуль при x = -2a (см. рис. 48):

Рис. 48

1) Пусть. На этом промежутке и поэтому данное уравнение примет вид

Найдем дискриминант полученного приведенного квадратного уравнения

значит, при любом действительном значении a уравнение имеет два различных действительных корня:

и

Выясним, входят ли они в промежуток Корень лежит в этой области только тогда, когда выполняется неравенство:

или

Последнее неравенство равносильно системе неравенств:

или

Последняя система неравенств не имеет решений, значит, ни при каком значении параметра a число не лежит в области

Корень лежит в рассматриваемой области тогда, когда выполнено неравенство:

или

Решим последнее неравенство. Ясно, что этому неравенству удовлетворяют все значения a из промежутка

При получим неравенство Отсюда находим:

Таким образом, при уравнение имеет единственное решение

2) Пусть На этом промежутке и поэтому исходное уравнение можно переписать в виде

Найдем дискриминант этого уравнения:

Уравнение не имеет решений, если т. е. если

Значит, уравнение не имеет корней для a из промежутка

Если a не принадлежат этому промежутку, то квадратное уравнение имеет корни причем при и Выясним теперь, при каких значениях параметра a найденные корни лежат в области

Для этого нужно решить неравенства и

Неравенство равносильно неравенству или совокупности двух систем неравенств:

(1) и (2)

Множество решений первой системы имеет вид вторая система не имеет решений. Значит, только при значении корень уравнения лежит в области

Неравенство равносильно неравенству или системе неравенств

Множество решений полученной системы неравенств есть отрезок

Только при этих значениях параметра a, корень принадлежит области: Таким образом, при данное уравнение в области решений не имеет.

Если то уравнение в рассматриваемой области имеет единственное решение

При значениях a, лежащих в области исходное уравнение имеет два различных корня и Если же то исходное уравнение имеет единственный корень Полученные результаты удобно свести в таблицу:

Значения a	Решения данного уравнения

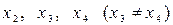
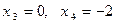
Таким образом, искомые значения a образуют два промежутка: и

Ответ:,

Пример 26. Найдите все значения параметра a из промежутка при каждом из которых больший из корней уравнения принимает наибольшее значение.

Решение

Преобразуем уравнение к виду

Значит, если тогда

Найдем наибольшее значение x, при котором т. е. наибольшее решение неравенства

Преобразуем это неравенство:

Последнее неравенство решим методом промежутков (см. рис. 49), помня, что

Рис. 49

Решение неравенства будет множество:

Ясно, что дробь принимает наибольшее значение при x = 6, тогда значение a будет равно:

Ответ: при a = 1.

Пример 27. Для каждого значения параметра a определите число решений уравнения

Решение

1. Если тогда уравнение не имеет решений, модуль любого вещественного числа неотрицателен.

2. Если тогда получим уравнение Это уравнение имеет два корня, так как

3. Если тогда получаем совокупность двух уравнений:

(1) и (2)

Первое уравнение имеет дискриминант:

Оно не будет иметь корней при но это невозможно, так как

Также оно не может иметь один корень (тогда a = -4, что также невозможно).

Таким образом, при уравнение (1) имеет два корня.

Второе уравнение имеет дискриминант:

Оно не будет иметь корней, если

Будет иметь один корень, если

Будет иметь два корня, если

Окончательно получаем.

Ответ:

1. Если тогда уравнение не имеет корней.

2. Если и тогда уравнение имеет два корня.

3. Если тогда уравнение имеет три корня.

4. Если тогда уравнение имеет четыре корня.

Пример 28. Найдите все значения параметра a, при каждом из которых уравнение имеет три различных корня; найдите эти корни:

Решение

Возведем обе части уравнения в квадрат:

Если тогда получим уравнение: (1)

Дискриминант этого уравнения равен:

Уравнение (1) будет иметь один корень, при и Два корня, при и

Если тогда получим уравнение: (2)

Дискриминант этого уравнения равен:

Уравнение (2) будет иметь один корень при и Два корни - при и

Делаем вывод, что при уравнение (1) имеет один корень, а уравнение (2) - два корня. При, уравнение (1) имеет два корня, а уравнение (2) - один.

Таким образом, при и данное уравнение имеет три корня.

Найдем эти корни. При, первое уравнение примет вид: Оно имеет один корень:

Уравнение (2) примет вид: которое имеет два корня:

При, уравнение (2) примет вид: Оно имеет один корень:

Уравнение (1) примет станет:

которое будет иметь корни:

Ответ: 1. При

2. При

Задание 6

1. Найти все значения параметра a, при каждом из которых уравнение имеет ровно два различных решения.

2. Найдите все значения параметра a из промежутка при каждом из которых меньший из корней уравнения принимает наименьшее значение.

3. Для каждого значения параметра a определите число решений уравнения

4. Найдите все значения параметра a, при каждом из которых уравнение имеет три различных корня; найдите эти корни:

Дата добавления: 2015-04-24