Отбор посторонних корней можно производить или путем сопоставления с множеством допустимых значений переменного, или путем проверки корней

Дробно-рациональные уравнения

Применяя основные теоремы о равносильности алгебраических уравнений, можно заменить дробно-рациональное уравнение целым алгебраическим уравнением. Но при этом, мы выполняем преобразования, которые могут привести к появлению посторонних корней.

Пример 1. Решите уравнение на множестве действительных чисел

.

Решение

Это уравнение дробно-рациональное. Прежде надо установить область допустимых значений переменной, что удобнее сделать, если разложить знаменатели дробей на множители:

Многочлен если имеет целые корни, то они будут находиться среди делителей свободного члена.

Делители свободного члена: .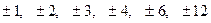

После проверки находим, что -2 и 2 являются корнями этого многочлена, значит он делится на произведение (x - 2)(x + 2), т. е. на .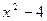

Разделив "уголком" данный многочлен на 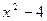получим в частном 2x + 3.

Таким образом, многочлен можно представить в виде произведения множителей: .

Два других знаменателя нетрудно разложить на линейные множители:

.

Уравнение примет вид:

.

Теперь достаточно найти наименьший общий знаменатель, а затем область допустимых значений.

Общий знаменатель: .

Область допустимых значений:

или

.

Преобразуем уравнение, умножив обе его части на общий знаменатель, который, по нашему требованию, не равен нулю. Попросту говоря, этот процесс называется ещё с младших классов "приведение к общему знаменателю", получим:

.

Оба корня входят в область допустимых значений, а значит являются решениями уравнениями.

Ответ: .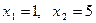

Задание 6

Решите уравнение на множестве действительных чисел.

1. . 2. .

3. .

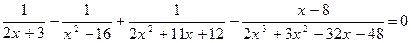Дата добавления: 2015-04-24