Алгебраические операции

Основные типы алгебраических структур

Алгебраические операции.

Темы курсовых работ и рефератов

1. Проблема общения в психологии.

2. Междисциплинарный подход к общению.

3. Педагогическое общение глазами психологов.

4. Основные функции педагогического общения.

5. Основные модели педагогического общения.

6. Особенности коммуникативной стороны общения в педагогическом процессе.

7. Основные механизмы межличностного восприятия в педагогическом процессе, их характеристика.

8. Социально-перцептивные стереотипы и особенности их проявления в учебном процессе.

9. Основные факторы социально-перцептивных искажений в учебном процессе.

10. Барьеры педагогического общения.

11. Личностные качества учителя, определяющие эффективность педагогического общения.

12. Коммуникативные способности.

13. Базовые умения профессионального общения учителя.

14. Стили педагогического общения.

15. Влияние характера педагогического общения на психическое развитие учащихся.

16. Дидактогения как психолого-педагогическая проблема.

Интернет-ресурсы (ссылки)

1. Лаборатория психосемантики и общения факультета психологии МГУ

2. Группа "Психология общения, развития и реабилитации личности" ПИ РАО

3. А. Иванова, Н.Н. Немцова, статья "Общение в педагогическом процессе"

Алгебра − наука об алгебраических операциях. Свойства множеств с алгебраическими операциями изучаются в этом параграфе.

Пусть X − произвольное множество.

Определение 1. 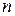-арной алгебраической операцией на X называется отображение 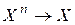. То есть 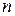– компонентному элементу однозначно ставится в соответствие элемент .

Задача. Пусть . Сколько 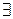n– арных алгебраических операций на ? Ответ. Таких операций

Алгебраические операции при называются унарными, при – бинарными, 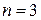– тернарными. Далее, как правило, будут рассматриваться бинарные операции.

Если 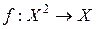, то пишут или 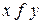. Операции на X обозначают символами . Последний символ используется для операции сложения, остальные − для операции умножения.

Определение 2. Множество X с конкретной алгебраической операцией называется алгебраической структурой.

На одном и том же множестве X могут быть заданы различные алгебраические структуры.

Примеры (алгебраических операций и алгебраических структур).

1. (R, +) − алгебраическая структура, и R имеем

2. (R, -) − алгебраическая структура.

3. (R, 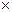) − алгебраическая структура.

4. Деление не является алгебраической операцией на R, так как не определено деление на нуль. Однако оно является алгебраической операцией на (R ).

5–8. То же самое для С.

9. (Rⁿ, +) − алгебраическая структура.

10. Скалярное произведение не является алгебраической операцией на множестве векторов, так как результатом операции является число.

11. – множество всех отображений относительно операции композиции является алгебраической структурой.

12. Как правило, алгебраическая операция на конечном множестве может быть задана с помощью таблицы Кэли, которая описывает результат операции на любой паре элементов множества. Рассмотрим множество, состоящее из 3-х элементов: {Доска, Окно, Тряпка} (кратко {Д, О, Т}). Введем следующую операцию, обозначаемую 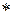(символ операции). Соответствующую таблицу Кэли можно выбрать в виде

2	Д	О	Т
Д	Д	О	Д
О	О	Д	Т
Т	Т	Т	Д

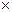13. Примерами тернарных операций на R³ R R 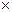R являются:

1) .

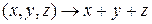2) .

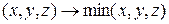3) .

Обычно рассматривают операции со специальными свойствами.

Определение 3. Бинарная операция на X называется коммутативной, если выполняется 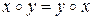; ассоциативной, если выполняется .

Замечание. Если 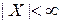(то есть множество – конечное) и − коммутативная операция, то таблица Кэли симметрична относительно диагонали.

Задача. Пусть . Сколько 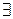коммутативных бинарных операций на X? Ответ. Таких операций .

Дата добавления: 2015-04-25