
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аудиторная работа. Монотонность функций. Экстремум
|
|
|
|
Монотонность функций. Экстремум. Наибольшее и наименьшее значения функции
Занятие 17
Ответы
Аудиторная работа
Правило Лопиталя–Бернулли. Формула Тейлора
Занятие 16
Ответы
15.9. а) 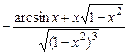 . б)
. б) 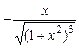 .
.
15.10. 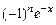 . 15.11. а)
. 15.11. а) 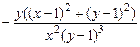 .
.
15.11. б) 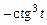 . 15.12. –1.
. 15.12. –1.
15.13. 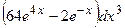 . 15.14. 1,93.
. 15.14. 1,93.
16.1. Применяя правило Лопиталя–Бернулли, найти пределы:
а) 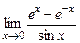 . б)
. б) 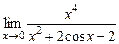 .
.
в) 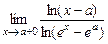 . г)
. г) 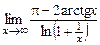 .
.
д) 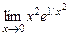 . е)
. е) 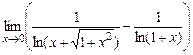 .
.
ж) 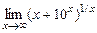 . з)
. з) 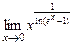 .
.
и) 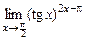 . к)
. к) 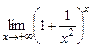 .
.
16.2. Разложить многочлен 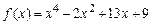 по степеням двучлена
по степеням двучлена 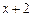 .
.
16.3. Написать формулу Тейлора 3-го порядка для функции 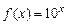 в точке
в точке 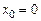 .
.
16.4. Вывести приближенную формулу 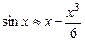 и оценить ее точность при
и оценить ее точность при  .
.
16.5. Вычислить с точностью до 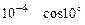 .
.
16.6. Найти пределы, используя разложение по формуле Тейлора:
а) 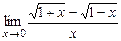 . б)
. б) 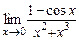 .
.
в) 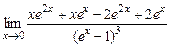 .
.
Домашнее задание
16.7. Найти пределы функций, применяя правило Лопиталя-Бернулли:
16.7. а) 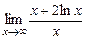 . б)
. б) 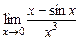 .
.
в) 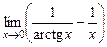 . г)
. г) 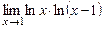 .
.
д) 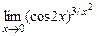 .
.
16.8. Написать формулу Тейлора 3-го порядка для функции 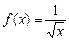 при
при 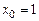 .
.
16.9. Вычислить приближенно 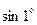 с точностью до
с точностью до 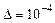 .
.
16.10. Вычислить предел 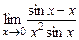 , используя формулу Тейлора с остаточным членом в форме Пеано.
, используя формулу Тейлора с остаточным членом в форме Пеано.
16.7. а) 1. б) 1/6. в) 0. г) 0. д) 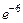 .
.
16.8. 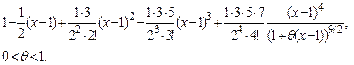
16.9. 0,0175. 16.10. 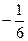 .
.
17.1. Найти интервалы монотонности и точки экстремума следующих функций:
а) 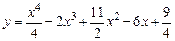 . б)
. б) 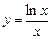 .
.
в) 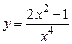 . г)
. г) 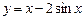 .
.
д) 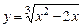 . е)
. е) 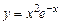
17.2. Найти экстремумы функций, пользуясь производной 2-го порядка:
а) 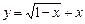 . б )
. б ) 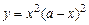 .
.
в) 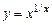 . г)
. г) 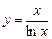 .
.
17.3. Определить наибольшее и наименьшее значения данных функций в указанных интервалах:
а) 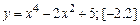 . б)
. б) 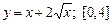 .
.
в) 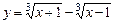 ;
; 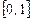 . г)
. г) 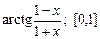 .
.
д) 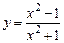 ;
; 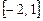 .
.
17.4. Требуется изготовить ящик с крышкой, объем которого был бы равен 72 см3, причем стороны основания относились бы как 1: 2. Каковы должны быть размеры всех сторон, чтобы полная поверхность ящика была наименьшей?
17.5. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
Домашнее задание
17.6. Найти интервалы возрастания и убывания и точки экстремума следующих функций:
а) 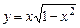 . б)
. б) 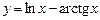 .
.
17.7. Найти экстремум функции 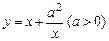 , используя вторую производную.
, используя вторую производную.
17.8. Найти наибольшее и наименьшее значения функций в указанных интервалах (или во всей области определения):
а) 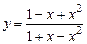 ;
; 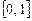 . б)
. б) 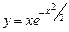 .
.
17.9. Из трех досок одинаковой ширины сколачивается желоб для подачи воды. При каком угле 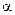 наклона боковых стенок к днищу желоба площадь поперечного сечения будет наибольшей?
наклона боковых стенок к днищу желоба площадь поперечного сечения будет наибольшей?
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 522; Нарушение авторских прав?; Мы поможем в написании вашей работы!