
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы линейной алгебры и аналитической геометрии 1 страница
|
|
|
|
Типовой расчет № 1
Ответы
Аудиторная работа
Выпуклость и вогнутость графиков функций. Асимптоты. Построение графиков функций
Занятие 18
Ответы
17.6. а) На 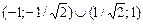 – убывает; на
– убывает; на 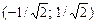 – возрастает;
– возрастает; 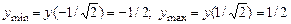 .
.
17.6. б) Возрастает на всей области определения.
17.7. 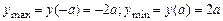 .
.
17.8. а) 1 и 3/5. 17.8. б) 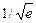 и
и 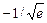 . 17.9.
. 17.9. 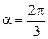 .
.
18.1. Найти точки перегиба и интервалы выпуклости и вогнутости графиков функций:
а) 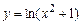 . б)
. б) 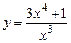 .
.
в) 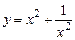 . г)
. г) 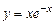 .
.
18.2. Найти асимптоты графиков функций:
а) 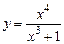 . б)
. б) 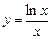 .
.
в) 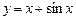 . г)
. г) 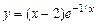 .
.
18.3. Провести полное исследование и построить графики функций:
а) 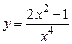 . б)
. б) 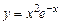 .
.
в) 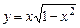 . г)
. г) 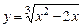 .
.
д) 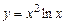 .
.
Домашнее задание
18.4. Найти точки перегиба графиков функций:
а) 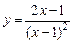 . б)
. б) 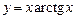 .
.
18.5. Найти асимптоты графика функции  .
.
18.6. Исследовать функции и построить их графики:
а) 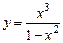 . б)
. б) 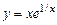 .
.
18.4. а) 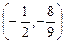 . б) Точек перегиба нет.
. б) Точек перегиба нет.
18.5. 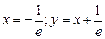 .
.
Задача 1
Исследовать систему уравнений и в случае совместности решить ее.
1.1. а) 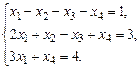 б)
б) 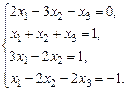
1.2. а) 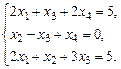 б)
б) 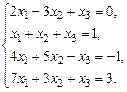
1.3. а) 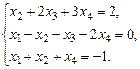 б)
б) 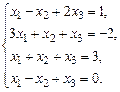
1.4. а) 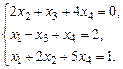 б)
б) 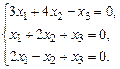
1.5. а) 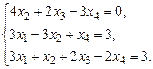 б)
б) 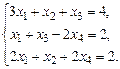
1.6. а) 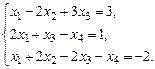 б)
б) 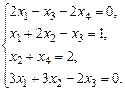
1.7. а) 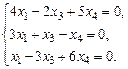 б)
б) 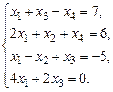
1.8. а) 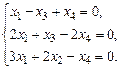 б)
б) 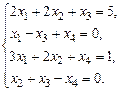
1.9. а) 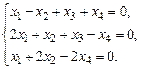 б)
б) 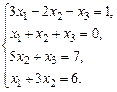
1.10. а) 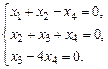 б)
б) 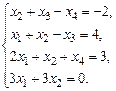
1.11. а) 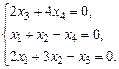 б)
б) 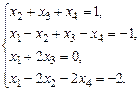
1.12. а) 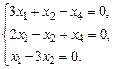 б)
б) 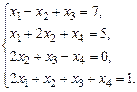
1.13. а) 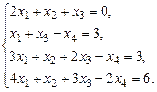 б)
б) 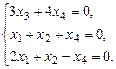
1.14. а) 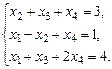 б)
б) 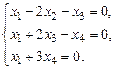
1.15. а) 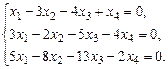 б)
б) 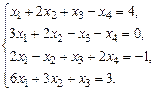
1.16. а) 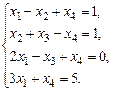 б)
б) 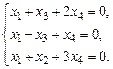
1.17. а) 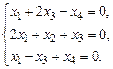 б)
б) 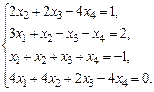
1.18. а) 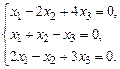 б)
б) 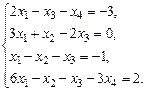
1.19. а) 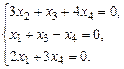 б)
б) 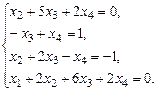
1.20. а) 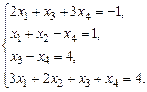 б)
б) 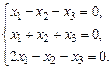
1.21. а) 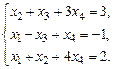 б)
б) 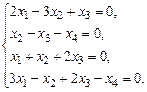
1.22. а) 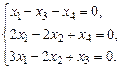 б)
б) 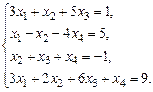
1.23. а) 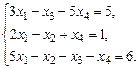 б)
б) 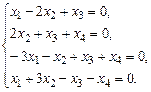
1.24. а) 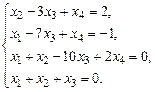 б)
б) 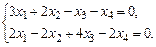
1.25. а) 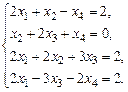 б)
б) 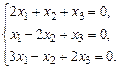
Задача 2
2.1. Вычислить 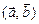 , где
, где 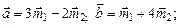
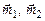 – единичные векторы, угол между которыми равен
– единичные векторы, угол между которыми равен 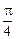 .
.
2.2. Найти проекцию вектора 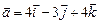 на направление вектора
на направление вектора 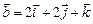 .
.
2.3. Найти 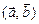 ,
, 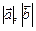 , если
, если 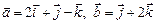 .
.
2.4. Вектор 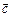 , коллинеарный вектору
, коллинеарный вектору  , образует острый угол с осью Oz. Найти координаты вектора
, образует острый угол с осью Oz. Найти координаты вектора 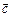 , если
, если 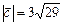 .
.
2.5. Найти 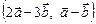 , если
, если 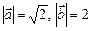 ,
, 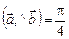 .
.
2.6. Найти 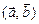 ,
, 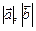 , если
, если 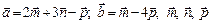 – ортогональный базис и
– ортогональный базис и 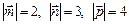 .
.
2.7. Найти длину вектора 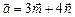 , если
, если 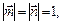
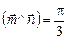 .
.
2.8. Найти вектор 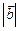 , коллинеарный вектору
, коллинеарный вектору 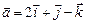 и удовлетворяющий условию
и удовлетворяющий условию 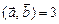 .
.
2.9. Найти 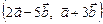 , если
, если 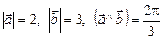 .
.
2.10. Вычислить синус угла между диагоналями параллелограмма, сторонами которого служат векторы 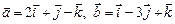 .
.
2.11. Найти вектор 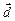 , удовлетворяющий условиям
, удовлетворяющий условиям 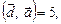
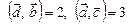 , если
, если 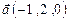 ,
, 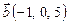 ,
, 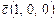 .
.
2.12. Даны векторы 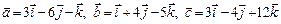 . Найти проекцию вектора
. Найти проекцию вектора 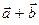 на направление вектора
на направление вектора 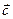 .
.
2.13. Вектор 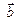 , коллинеарный вектору
, коллинеарный вектору 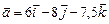 , образует острый угол с осью Oz. Найти координаты вектора
, образует острый угол с осью Oz. Найти координаты вектора 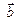 , если
, если 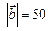 .
.
2.14. Найти площадь треугольника, построенного на векторах 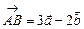 и
и 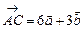 , если
, если 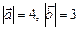
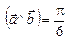 .
.
2.15. Найти 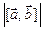 , если
, если 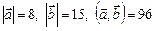 .
.
2.16. Какой угол образуют векторы 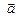 и
и 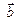 , если
, если 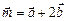 и
и 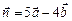 ортогональны,
ортогональны, 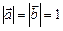 ?
?
2.17. Вычислить 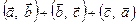 , если
, если 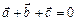 ,
, 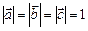 .
.
2.18. Даны точки А (–5, 7, –6) и B (7, –9, 9). Найти проекцию вектора 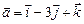 на направление вектора
на направление вектора 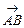 .
.
2.19. Найти координаты вектора 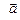 , если
, если 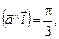
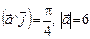 .
.
2.20. Найти вектор 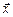 , ортогональный вектору
, ортогональный вектору 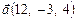 , имеющий с ним одинаковую длину и лежащий в плоскости Oyz.
, имеющий с ним одинаковую длину и лежащий в плоскости Oyz.
2.21. Найти угол между векторами 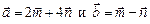 , если
, если 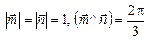 .
.
2.22. Найти проекцию вектора 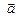
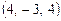 на направление вектора
на направление вектора 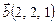 .
.
2.23. Какой угол образуют единичные векторы 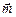 и
и 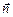 , если векторы
, если векторы 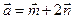 и
и 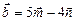 ортогональны?
ортогональны?
2.24. Доказать, что скалярное произведение двух векторов не изменится, если к одному из них прибавить вектор, ортогональный другому сомножителю.
2.25. При каких значениях a и b векторы 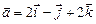 и
и 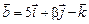 коллинеарны?
коллинеарны?
Задача 3
3.1. Найти 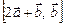 , где
, где 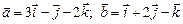 .
.
3.2. Вычислить площадь параллелограмма, построенного на векторах 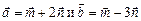 , если
, если 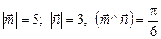 .
.
3.3. Вектор 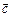 перпендикулярен векторам
перпендикулярен векторам 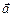 и
и 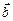 , угол между
, угол между 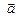 и
и 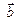 равен
равен 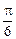 . Зная, что
. Зная, что 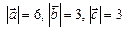 , вычислить
, вычислить 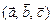 .
.
3.4. Найти 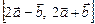 , где
, где 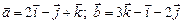 .
.
3.5. Найти вектор 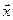 , если известно, что он ортогонален векторам
, если известно, что он ортогонален векторам 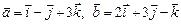 и
и 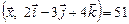 .
.
3.6. Найти координаты вектора 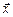 , если он ортогонален векторам
, если он ортогонален векторам 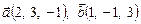 и
и 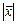 =1.
=1.
3.7. Найти единичный вектор 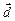 , компланарный векторам
, компланарный векторам 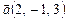 и
и 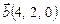 и ортогональный вектору
и ортогональный вектору 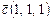 .
.
3.8. Вычислить площадь параллелограмма, сторонами которого являются векторы 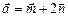 и
и 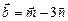 , если
, если 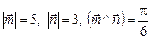 .
.
3.9. Вычислить синус угла между диагоналями параллелограмма, сторонами которого служат векторы 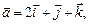
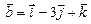 .
.
3.10. Вычислить высоту параллелепипеда, построенного на векторах 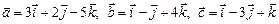 , если за основание взят параллелограмм, построенный на векторах
, если за основание взят параллелограмм, построенный на векторах 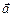 и
и 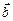 .
.
3.11. Вектор 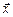 , перпендикулярный векторам
, перпендикулярный векторам 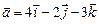 и
и 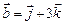 , образует с осью Oy тупой угол. Найти координаты вектора
, образует с осью Oy тупой угол. Найти координаты вектора 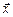 , если
, если 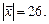
3.12. Вычислить площадь параллелограмма, сторонами которого являются векторы 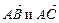 , если
, если 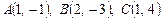 .
.
3.13. Вершины треугольной пирамиды находятся в точках 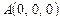 ,
, 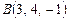 ,
, 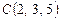 ,
, 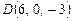 . Найти длину высоты, проведенной из вершины А.
. Найти длину высоты, проведенной из вершины А.
3.14. Проверить, лежат ли точки 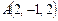 ,
, 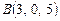 ,
, 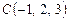 ,
, 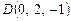 в одной плоскости.
в одной плоскости.
3.15. Проверить, компланарны ли векторы 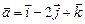 ,
, 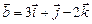 ,
, 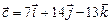 .
.
3.16. Дана треугольная пирамида с вершинами 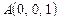 ,
, 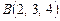 ,
, 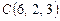 ,
, 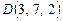 . Найти длину высоты пирамиды, проведенной на грань BCD.
. Найти длину высоты пирамиды, проведенной на грань BCD.
3.17. Найти площадь параллелограмма, сторонами которого являются векторы 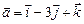 и
и 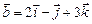 .
.
3.18. Найти 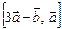 , если
, если 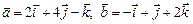 .
.
3.19. Найти 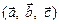 , если векторы
, если векторы 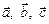 образуют правую тройку и взаимно перпендикулярны,
образуют правую тройку и взаимно перпендикулярны, 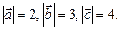
3.20. Показать, что точки A (3, 1, –1), B (5, 7, –2), C (1, 5, 0) и
D (9, 4, –4) лежат в одной плоскости.
3.21. Вычислить площадь параллелограмма, построенного на векторах 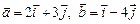 .
.
3.22. Найти единичный вектор, ортогональный векторам 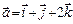 и
и 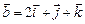 .
.
3.23. Вершинами треугольной пирамиды являются точки A (-5, 4, 8), B (2, 3, 1), C (4, 1, –2) и D (6, 3, 7). Найти длину высоты, проведенной на грань BCD.
3.24. Вычислить синус угла между диагоналями параллелограмма, построенного на векторах 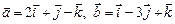 .
.
3.25. Проверить, лежат ли точки A (–1, 2, 3), B (0, 4, –1), C (2, 3, 1) и D (–2, 1, 0) в одной плоскости.
Задача 4
4.1. Написать уравнение прямой, проходящей через начало координат перпендикулярно прямой 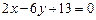 .
.
4.2. Найти угол между прямой 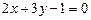 и прямой, проходящей через точки
и прямой, проходящей через точки 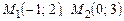 .
.
4.3. Найти уравнение прямой, проходящей через точку 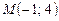 параллельно прямой
параллельно прямой 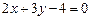 .
.
4.4. Дан треугольник с вершинами в точках 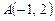 ,
, 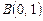 и
и 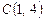 . Написать уравнение прямой, проходящей через вершину А параллельно противоположной стороне.
. Написать уравнение прямой, проходящей через вершину А параллельно противоположной стороне.
4.5. При каком значении параметра α прямые 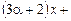
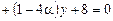 и
и 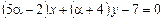 взаимно перпендикулярны?
взаимно перпендикулярны?
4.6. Даны вершины треугольника 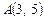 ,
, 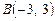 и
и  . Определить длину медианы, проведенной из вершины С.
. Определить длину медианы, проведенной из вершины С.
4.7. При каких значениях α прямые 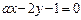 и
и 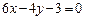 :
:
а) параллельны; б) имеют одну общую точку?
4.8. Написать уравнение прямой, проходящей через точку 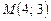 перпендикулярно вектору
перпендикулярно вектору 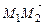 , если
, если 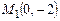 ,
, 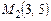 .
.
4.9. Дан треугольник с вершинами в точках 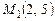 ,
, 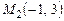 и
и 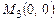 . Составить уравнение медианы, проведенной из вершины
. Составить уравнение медианы, проведенной из вершины 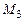 .
.
4.10. Найти уравнение прямой, проходящей через точку 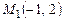 перпендикулярно прямой, соединяющей точки
перпендикулярно прямой, соединяющей точки 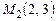 и
и 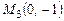 .
.
4.11. На прямой 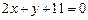 найти точку, равноудаленную от двух данных точек
найти точку, равноудаленную от двух данных точек 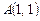 и
и 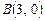 .
.
4.12. Написать уравнение прямой, проходящей через точку 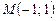 параллельно прямой
параллельно прямой 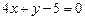 .
.
4.13. Найти расстояние между прямыми 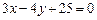 и
и 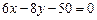 .
.
4.14. Найти уравнение прямой, проходящей через точку 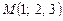 параллельно вектору
параллельно вектору 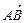 , если
, если 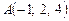 ,
, 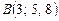 .
.
4.15. Привести к каноническому виду уравнения прямой
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 538; Нарушение авторских прав?; Мы поможем в написании вашей работы!