Второе правило

Первое правило

Расчет цепей с помощью законов кирхгофа.

алгебраическая сумма токов в каждом узле любой цепи равна нулю

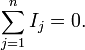
алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура

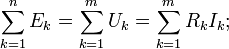
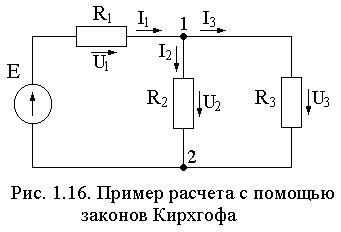
независимым узлом называется узел, в который входит хотя бы одна ветвь, не входящая в другие узлы. если число узлов обозначим через к, то число независимых узлов равно (к –1). на схеме (рис. 1.16) из двух узлов только один независим.

независимым контуром называется контур, который отличается от других контуров хотя бы одной ветвью, не входящей в другие контура. в противном случае такой контур называется зависимым.

если число ветвей цепи равно n, то число независимых контуров равно [ n – (к –1)].

в схеме (рис. 1.16) всего три контура, но только два независимых контура, а третий – зависим. выделять независимые контура можно произвольно, т. е. в качестве независимых контуров можно выбрать при первом расчете одни, а при втором расчете (повторном) – другие, которые раньше были зависимыми. результаты расчета будут одинаковыми.

если по первому закону кирхгофа составить уравнения для (к –1) независимых узлов, а по второму закону кирхгофа составить уравнения для [ n – (к –1)] независимых контуров, то общее число уравнений будет равно:

(K –1) + [ n – (K –1)] = n.

Это означает, что для расчёта имеется необходимое число уравнений.

Последовательность расчёта:

1. Расставляем условно – положительные направления токов и напряжений.(n=3)

2. Выбираем независимые узлы и независимые контура. С помощью первого закона Кирхгофа составляем (К –1) уравнений для независимых узлов В схеме два узла, следовательно, из них только один независимый. В качестве независимого узла выберем узел 1. Для него запишем уравнение по первому закону Кирхгофа:

I ₁ = I ₂ + I ₃.

3. С помощью второго закона Кирхгофа составляем [ n – (К –1)] уравнений для независимых контуров. При этом напряжения на элементах выражаются через токи, протекающие через них. В схеме всего три контура, но независимых только два. В качестве независимых контуров выберем контур из элементов E – R ₁– R ₂ и контур из элементов R ₂– R ₃. Обходя эти два контура по направлению движения часовой стрелки, записываем следующие два уравнения:

E = I ₁, R ₁ + I ₂ R ₂,

0 = – I ₂ R ₂ + I ₃ R ₃ .

6. Решаем составленную систему уравнений и определяем токи в ветвях. При получении отрицательных значений для некоторых токов, необходимо их направления в схеме изменить на противоположные, которые и являются истинными.

Решаем полученные три уравнения и определяем токи в ветвях. Затем через найденные токи по закону Ома определяем падения напряжений на всех элементах цепи.

Дата добавления: 2015-05-06