Основные теоретические положения. Методы исследования электрических цепей постоянного тока

Методы исследования электрических цепей постоянного тока

Лабораторная работа 2

Цель работы. Получить навыки расчёта разветвлённых электрических цепей постоянного тока известными методами. Освоить принцип и технику выполнения расчётов, особенности и целесообразность применения методов в конкретных случаях.

Для расчёта разветвлённых электрических цепей разработано несколько методов:

- метод эквивалентных преобразований

- метод применения законов Кирхгофа,

- метод контурных токов,

- метод узловых потенциалов,

- метод наложения током (метод суперпозиции),

- метод эквивалентного генератора (метод холостого хода и короткого замыкания).

Рассмотрим некоторые методы исследования электрических цепей постоянного тока.

Метод контурных токов

Метод контурных токов (метод Максвелла) напоминает метод расчета с использованием законов Кирхгофа. Однако он проще, поэтому получил большее распространение на практике при расчетах разветвлённых цепей, состоящих из n независимых контуров. Определение токов в ветвях сводится к решению системы n = р - q + 1 уравнений для контурных токов I_1k, I_2k, I_nk; (где p- число ветвей, q – узлов). Действительный ток в каждой ветви находится как алгебраическая сумма контурных токов, протекающих через соответствующую ветвь. Выбор направлений контур­ных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один из анализируемых контуров.

Для иллюстрации метода рассмотрим электрическую цепь

(рис. 2.1)

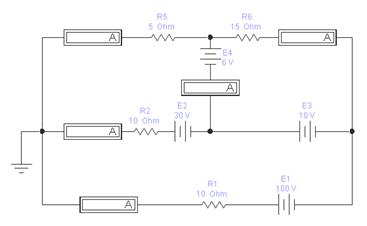
Рис.2.1.

В представленной схеме – три независимых контура

Составим систему уравнений для контуров:

El - Е2 - ЕЗ = I_lk(Rl + R2) – I_2kR2;

Е2 - Е4 = I_2k(R2 + R5 + R4) - I_3kR4 - I_lkR2;

ЕЗ - E4 = I_3k(R6 + R4) + I_2kR4.

Решение этой системы уравнений, позволяет определить токи в контурах: I_ik = 5 A, I_2k = 4 A, I_3k = -2 А.

Далее можно определить истинные токи во всех ветвях.

В ветви, где действует ЭДС Е1, истинный ток I1 имеет направление контурного тока I_!k и равен ему: I1 = Ii_k = 5 А.

В ветви с сопротивлением R5 истинный ток I5 имеет направление контурного тока I_2k и равен ему: 15 = I_2k = 4 А.

В ветви с R6 ис­тинный ток I6 имеет направление, противоположное контурному току 1₃к, и ра­вен I6 = - I_3к = 2 А.

В ветви с R2 истинный ток I2 получится на­ложением контурных токов I_1К и I_2k, а направление - большего из них:

12 = I_1k - I_2k = 1А.

В ветви с R4 истинный ток I4 получится наложением контурных токов I_2k и I_3k и - направление большего из них, т. е. I4 = I_2k + I_3k = 4 + (-2) = 2 А.

В ветви, где действует ЭДС ЕЗ, истинный ток I3 получится наложением контурных токов I|_k и I_3k и будет иметь направле­ние тока I,_k, т. е. I3 = Iik + I₃k = 5 + (-2) = 3 А.

Контрольные вопросы и задания

1. В чем отличие метода контурных токов от метода расчета с ис­пользованием законов Кирхгофа для аналогичных цепей?

2. Выполните расчет токов в ветвях схемы на рис.2.1. методом контурных токов при Е1 = 50 В, Е2 = 15 В, ЕЗ = 5 В и Е4 = 3 В.

3. Сравнить полученные данные с результатами моделирования.

Метод суперпозиции (наложения).

При реализации этого метода ток в любой ветви схемы с несколькими источниками ЭДС рассчитывается как алгебраическая сумма токов, вызываемых в ней каждой ЭДС в отдельности. При этом предполагается, что при анализе воздействия одной ЭДС остальные прини­маются равными нулю и при расчетах учитываются только их внутренние сопротивления.

При использовании метода наложения потребуются некоторые навыки в преобразовании электрических цепей. Во всех случаях замена одних схем другими - эквивалентными им, не должна приводить к изменению токов и напряжений на участках цепи, не подвергшихся преобразованию. Наиболее часто употребляемые преобразования цепей сводятся к следующим:

1.Замена последовательно включённых сопротивлений одним эквивалентным.

Rэкв цепи, состоящей из последовательно соединенных сопротивлений R₁, R₂...,R_n. равно сумме этих сопротивлений:

Rэкв = R 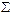= 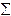Ri = R₁ + R₂ +... + R_n

2. Замена параллельных сопротивлений одним эквивалентным.

При параллельном соединении сопротивлений эквивалентное сопротивление Rэкв цепи определяется из условия суммирования проводимостей: 1/Rэкв = 1/R₁ + 1/R₂ +... + 1/R_n.

В случае двух параллельно соединенных сопротивлений R₁//R₂ :

Rэкв = R₁R₂/(R₁ + R₂).

З. При исследовании разветвлённых электрических цепей возникает необходимость преобразования соединения резисторов «треугольником» в эквивалентную «звезду» и обратные преобразования: «звезда» / «треугольник».

Формулы преобразований имеют следующий вид:

Rl = R12 • R31/A; R2 = R23 • R12/A; R3 = R31• R23/A;

R12 = R1 + R2 + R1R2/R3;

R23 = R2 + R3 + R2-R3/R1;

R31 = R3 + Rl + R3 • R1/R2,

где А = R12 + R23 + R13.

Применим метод наложения к расчёту конкретной схемы.

В схеме на рис 2.2 - три независимых контура и два источника ЭДС. Все источники напряжения идеальны, поэтому их внут­ренние сопротивления равны нулю (Rвн=0).

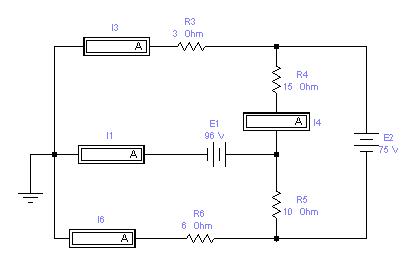
Рис.2.2

На первом этапе предположим, что действует только ЭДС Е1, а вместо Е2 будет просто проводник (Rвн=0). В этом случае ЭДС Е1 нагружена на эквивалентное сопротивление

R_1ЭKB = R3 • R6/(R3 + R6)+ + R4 • R5/(R4 + R5) = 8 Ом.

При этом токи в ветвях составят:

I1' = Е1/R_1ЭKB = 96/8 =12 А; I3' = I1'R6/(R3 + R6) = 12-6/9 = 8 А;

I4' = I1' R5/(R4+R5) =12•10/25 = 4,8А; 12'=I3'-14'=8 - 4,8= 3,2А;

I6' = I1' - 13' = 12 - 8 = 4 А; 15' = I1' -14' = 12 - 4,8 = 7,2 А.

На втором этапе расчёта предположим, что активным источником является ЭДС Е2, а источник Е1 - закоро­чен.

В этом случае ЭДС Е2 нагружена на эквивалентное сопротивление

R2_3KB = R3(R4/(R3 + R4) + R5(R6/(R5 + R6) = 6,25 Ом.

При этом токи в ветвях име­ют следующие значения:

I2" = E2/R2_3KB = 75/2,5 = 12 А;

I3" = I2"R4/(R3 + R4) = 12 • 15/18 = 10 А;

I6"=I2"R5/(R5 + R6) = 12- 10/16 = 7,5 А;

I1" = 13" - 16" = 10-7,5 = 2,5 А;

I4" = 12" - 13" = 12 - 10 = 2 А; 15" = 12" -16" = 12 - 7,5 = 4,5 А.

Складывая алгебраически токи, от действия каждой ЭДС в отдельности, найдем истинные токи в каждой ветви:

I1= I1'+I1" = 12 + 2,5 = 14,5 А;

I2 = 12' + 12" = 3,2 +12= 15,2А;

I 3 = 13' + 13" = 8 + 10 = 18 А;

I 4 = 14' - 14" = 4,8 - 2 = 2,8 А;

I 5 = 15" + 15" = 7,2 + 4,5 = 11,7 А;

I6 = 16" - 16' = 7,5 - 4 = 2,5 А,

что совпада­ет с результатами моделирования.

Контрольные вопросы и задания

1. Какие законы используются при расчете токов ветвей методом наложения?

2. В каких случаях целесообразен метод наложения?

3.Выполните расчет токов в ветвях схемы на рис. 2.2, в методом наложения при Е1 = 48 В, Е2 = 45 В. Сравните полученные данные с результатами моделирования.

3. Выполните расчет токов в ветвях схем на рис. 2.1. методом наложения и про­верьте результаты расчета путем моделирования.

Метод эквивалентного генератора

Метод эквивалентного генератора напряжения называют методом ко­роткого замыкания и холостого хода или методом активного двухполюсника. С его помощью определяют ток в определенной ветви схемы. Назовем ее АВ и предположим, что исследуемая ветвь содержит одно сопротивление R. Для нахождения тока в этой ветви размыкают ветвь и любым из рассмотренных выше методов определя­ют разность потенциалов U_xx на зажимах А,В в разомкнутой ветви (режим холосто­го хода). Затем вычисляют сопротивление короткого замыкания R_K3, равное эк­вивалентному сопротивлению остальной цепи. При этом имеющиеся в схеме ис­точники должны быть выключены и заменены их внутренними сопротивлениями, а питание схемы осуществляется от постороннего источника, подключенного к зажимам А,В исследуемой ветви. Следующим этапом является режим короткого замыкания (р.к.з.), при котором определяется ток I_КЗ в ветви АВ при закороченных зажимах А, В. Следует заметить, что этот этап не обязателен, если сопротивление R_K3 удаётся определить более простым способом. Если режим короткого замыкания применить, то в этом случае R_K3 = U_XX/I_K3.

И искомый ток в ветви определяется из выражения:

I = U_XX/(R+R_K3).

Применение метода рассмотрим на конкретном примере:

На рис.2.3 представлена мостовая схема, состоящая из двух плеч, образованных резисторами Rl, R2 и R3, R4

В одну диагональ моста - диагональ питания - включён источник напряжения Еп и переключатель, управляемый клавишей Е клавиатуры, в другую – измерительную диагональ — включён резистор R5 с ключом X (управление клавишей X).

В задаче требуется определить силу тока через резистор R5 в рабочем состоянии (ключ Х замкнут).

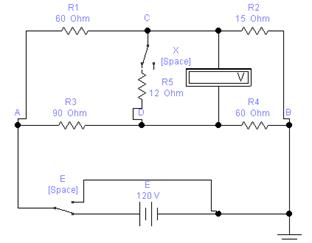
Рис.2.3.

На первом этапе моделирования реализуется режим холостого хода: ключ Х ветви СD – разомкнут. В этом режиме через сопротивления Rl, R2 протекает ток I*, а через сопротивления R3, R4 — ток I**, которые равны соответственно:

I* = E/(R1 + R2)= 120/75 = 1,6 А;

I** = E/(R3 + R4) = 120/150 = 0,8 А.

При этом потенциалы в точках С и D определяются падениями напряжений на резисторах R1 и R3:

Uас = I* R1 = 1,6 • 60 = 96 В; Uad = I** R3 = 0,8 • 90 = 72 В.

Располагая значением потенциалов в точках С и D, нетрудно найти и напряжение между ними, которое равно напряжению холостого хода: U_C d = Uxx = Ua_C - Uad = 96 - 72 = 24 В.

На втором этапе моделирования следует определить сопротивление короткого замыкания.

Cделать это можно двумя способами:

1. Путем непосредственного расчета с использованием данных схемы. В этом случае источник Е нужно выключить, оставив его внутреннее сопротивление, равное в данном случае нулю. Сопротивление короткого замыкания будет равным сопротивлению цепи между точками С и D:

R_K3 = Rl • R2/(R1 + R2) + R3 • R4/(R3 + R4) = 48 Ом.

Для реализации этого режима необходимо в схеме рис. 2.3, ключ Е перевести в верхнее положение, зашунтировав источник питания Е,и мультиметром измерить сопротивление в точках СD.

2. Искомое сопротивление можно найти другим путем. Для этого нужно замкнуть точки С и D накоротко, вычислить ток I_K3 протекающий через коротко замкнутый участок, и сопротивление короткого замыкания определить из выражения: R_K3 = U_XX/I_K3

Для моделирования такого режима необходимо ключ Е вернуть в исходное состояние, а мультиметр перевести в режим амперметра.

При этом измерить ток короткого замыкания I_{K3 =} 0,5 А. Откуда определяют R_K3 = 24/0,5 = 48 Ом.

Теперь можно определить и искомый ток, используя приведённое выше выражение:

I5 = U_XX/(R5 + Rk) = 24/(12 + 48) = 0,4 А.

Для моделирования рабочего режима ключ X необходимо замкнуть и мультиметром в режиме вольтметра измерить

U_XX = 4,8 В. Следовательно ток в цепи равен 4,8/12 = 0,4 А,

Для закрепления метода выполнить индивидуальные задания:

Контрольные вопросы и задания

1. Какие законы теории цепей используются в методе эквивалентного генератора

2. Проведите расчеты и моделирование рассмотренной мостовой схемы во всех режимах при сопротивлении резистора R5 = 6 Ом.

3. Рассчитайте ток через сопротивление R2 рассмотренной схемы методом эквива­лентного генератора напряжения, сопровождая расчет моделированием.

Дата добавления: 2015-05-06