
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоретические положения. Трехфазные электрические цепи синусоидального тока
|
|
|
|
Лабораторная работа 5
Трехфазные электрические цепи синусоидального тока
Цель работы. Исследование режимов работы симметричного и несимметричного потребителей электрической энергии в трехфазных электрических цепях, определение основных соотношений между фазными и линейными значениями токов и напряжений при симметричной нагрузке и включении потребителей звездой и треугольником.
В качестве трехфазных источников напряжений на электрических станциях используют трехфазные синхронные генераторы, на статоре которых размещаются три фазные обмотки (фазы), смещенные в пространстве относительно друг друга на угол 120°. При вращении ротора, выполненного в виде электромагнита постоянного тока, в обмотках генератора будут индуцироваться переменные ЭДС, сдвинутые относительно друг друга по фазе также на 120° (2 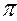 /3):
/3):
еа = Еат sin 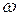 t
t
ев = Евт sin(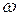 t - 2
t - 2 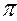 /3)
/3)
ес = Ест sin(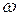 t + 2
t + 2 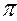 /3),
/3),
где Еат = Евт = Ест = Ет—значения ЭДС фаз А, В, С.
Под действием трехфазной системы ЭДС на зажимах трехфазного потребителя создается трехфазная симметричная система напряжений, сдвинутых по фазе на угол 120°, т. е. на угол 2 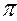 /3, и имеющих одинаковые амплитудные и действующие значения Uab = Ubc = Uca (векторная диаграмма представлена на рис. 5.1. В трехфазной системе потребители электроэнергии соединяются звездой или треугольником. Передача электрической энергии к потребителю в трехфазной трехпроводной системе осуществляется с помощью линейных проводов
/3, и имеющих одинаковые амплитудные и действующие значения Uab = Ubc = Uca (векторная диаграмма представлена на рис. 5.1. В трехфазной системе потребители электроэнергии соединяются звездой или треугольником. Передача электрической энергии к потребителю в трехфазной трехпроводной системе осуществляется с помощью линейных проводов
В четырехпроводной трехфазной системе имеется четвертый — нейтральный (Nn) провод, соединяющий общие точки фаз источника N и потребителя п.
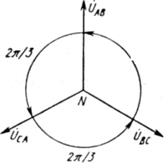
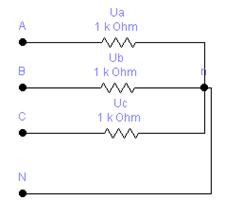
Рис.5.1
Рис.5.2
Соединение, при котором концы фаз потребителя объединяют в общую точку п, называемую нейтральной точкой, а начала фаз подсоединяют к трехфазному источнику питания посредством линейных проводов, называется соединением звездой (рис.5.2). Токи Ia, Ib и Iс в соответствующих линейных проводах называются линейными,
токи, протекающие по фазам, — ф а з н ы м и,
а ток In в нейтральном проводе — нейтральным.
При рассмотрении трехфазной системы считают, что трехфазный источник является симметричным, фазные напряжения которого равны между собой и сдвинуты по фазе относительно друг друга на угол 2 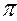 /3. Напряжения между линейными проводами потребителя Uab, Ubc и Uса называются линейными, а между началом и концом фаз потребителя, включенного звездой, Ua, Ub Ucc — фазными.
/3. Напряжения между линейными проводами потребителя Uab, Ubc и Uса называются линейными, а между началом и концом фаз потребителя, включенного звездой, Ua, Ub Ucc — фазными.
Из схемы рис. 5.2 видно, что при соединении потребителя звездой по его фазам протекают те же токи 1 а, 1 в и 1 с, что и по линейным проводам: фазные токи оказываются равными соответствующим линейным токам: Iф = I.л
При этом по первому закону Кирхгофа для нейтральной точки п можно записать 1А + 1В + 1С = In
При соединении потребителя звездой, независимо от величины и характера сопротивлений его фаз, а также от того, имеется или отсутствует нейтральный провод, между линейными и фазными напряжениями потребителя существуют соотношения, полученные по второму закону Кирхгофа:
Uав=Uа –Uв, UBC=Ub - Uc, Ucа=Uc - Ua
Нагрузка, при которой сопротивления всех фаз потребителя равны между собой {Zа,=Zb=Zс), называется симметичной
При этомRa=Rb=Rc Ха =Хb=Хс; Uab = Ubc =Uca
Сопротивления линейных проводов обычно малы и ими можно пренебречь. Линейные напряжения генератора равны линейным напряжениям потребителя, фазные напряжения генератора равны фазным напряжениям потребителя. При этом, линейные напряжения потребителя, как и фазные, сдвинуты относительно друг друга на угол 2л/3 (рис5.3)
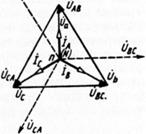
Рис. 5.3
При соединении потребителя звездой при симметричной нагрузке между фазными и линейными напряжениями существует соотношение: Uл = 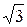 Uф
Uф
Фазные токи потребителя определяют по закону Ома:
IA = Ua /Za, IB = Ub /Zb, Ic = Uc /Zc.
При этом напряжение между нейтральными токами UnN =0. Фазные токи при симметричной нагрузке также равны между собой Ia = Ib =Ic =Iф и сдвинуты относительно фазных напряжений на равные углы 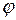 а =
а = 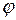 в =
в = 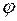 с =
с = 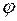 ф,
ф,
где: tg 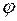 а = Ха/Ra = tg
а = Ха/Ra = tg 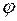 в = Хв/Rв =
в = Хв/Rв = 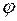 с = Хс/Rс.
с = Хс/Rс.
При симметричной нагрузке ток в нейтральном проводе, определяемый как векторная сумма фазных токов, оказывается равным нулю. При несимметричной нагрузке комплексные сопротивления всех трех фаз в общем случае не равны между собой: Za 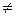 Zb
Zb 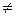 Zс.
Zс.
Пренебрегая сопротивлениями проводов, можно считать, что линейные напряжения потребителя независимо от характера нагрузки равны линейным напряжениям генератора, т. е. система линейных напряжений и при несимметричной нагрузке симметрична.
При включении нейтрального провода к несимметричной нагрузке потенциал нейтральной точки потребителя п равен потенциалу нейтральной точки N генератора
При наличии нейтрального провода и несимметричной нагрузки сумма фазных токов трехфазной системы в соответствии с первым законом Кирхгофа для нейтральной точки равна току в нейтральном проводе 1а+1в+Iс =IN 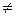 0.
0.
При этом векторная диаграмма для несимметричной нагрузки с нейтральным проводом имеет вид, представленный на рис. 5.4.
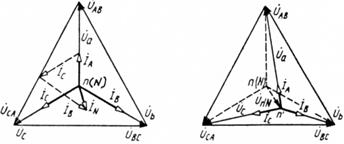
Рис 5.4. Рис. 5.5
При отключении нейтрального провода потенциал нейтральной точки п потребителя не равен потенциалу нейтральной точки N генератора. При этом нейтральная точка п на векторной диаграмме потребителя сместится из своего первоначального положения в другое (пi), при котором геометрическая сумма фазных токов потребителя равна нулю: 1а+1в+Iс=0.
В этом случае векторная диаграмма принимает вид, представленный на рис.5.5, Как видно,при несимметричной нагрузке в трехфазной системе без нейтрального провода фазные напряжения потребителя оказываются не равными друг другу. При этом на одних фазах может быть напряжение пониженное, на других — повышенное, по сравнению с фазными напряжениями генератора, В этом случае между фазными токами, напряжениями и сопротивлениями существуют те же соотношения, обусловленные законом Ома, что и при симметричной нагрузке.
Частные случаи работы трёхфазной цепи - замыкание или обрыв одной фазы нагрузки рассмотреть самостоятельно.
Соединение, при котором конец первой фазы х соединяется с началом второй b, конец второй y - с началом третьей c, а конец третьей z - с началом первой а, называется соединением трехфазного потребителя треугольником
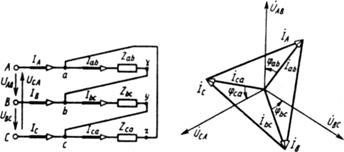
Рис. 5.6 Рис. 5.7
При этом начала всех фаз потребителя присоединяют к источнику электрической энергии с помощью линейных проводов. Из рис. 5.6 видно, что каждая фаза потребителя присоединяется соответственно к двум линейным проводам. Поэтому при соединении потребителя треугольником фазные напряжения оказываются равными соответствующим линейным напряжениям: Uф =Uл. Фазные токи при соединении треугольником не равны линейным, так как в начале каждой фазы потребителя имеется узел разветвления токов. При этом независимо от сопротивлений потребителя между фазными и линейными токами существуют соотношения, определяемые на основании первого закона Кирхгофа для узлов разветвления токов: IA = Iab~Ica IB = Ibc - Iab, IC = Ica—Ibc
Пользуясь указанными соотношениями, по векторам фазных токов, Iab, Ibc, Ica можно построить векторы линейных токов IA, IB, IC
Соотношения между фазными напряжениями, токами и сопротивлениями при соединении потребителя треугольником находят в соответствии с законом Ома:
Iab = Uab / Zab; Ibc = Ubc /Zbc; Ica,=Uca / Zca
На рис. 5.6 – 5.12 принято: Zab=Rab, Zbc=Rbc, Zca=Rca
Углы сдвига по фазе между векторами фазных напряжений, Uab, Ubc, Uca соответствующих фазных токов Iab, Ibc, Ica определяются фазными сопротивлениями потребителя:
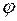 аb =arctgXab/Rab;
аb =arctgXab/Rab; 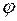 bc = arctgXbc/Rbc;
bc = arctgXbc/Rbc; 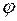 cа = arctgXca/Rca
cа = arctgXca/Rca
При симметричной нагрузке комплексные сопротивления всех трех фаз одинаковы, т. е. Zab = Zbc = Zса.
При этом как актив ные, так и реактивные сопротивления фаз потребителя равны: Rab = Rbc = Rca', Хab = Хbс = Хca,
причем реактивные сопротивления имеют одинаковый (индуктивный или емкостный) характер. В этом случае фазные токи и соответствующие углы сдвига по фазе между фазными напряжениями и фазными токами будут равны между собой: 1ав=1вс =1са = Iф, 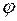 ав =
ав = 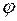 вс =
вс = 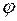 са =
са = 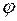 ф
ф
Из векторной диаграммы для симметричной нагрузки при соединении потребителя треугольником, представленной на
рис. 5.7, видно, что линейные токи оказываются равными и сдвинутыми относительно друг друга по фазе на угол 2я/3. При этом между фазными и линейными токами существует соотношение: Iл = 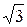 Iф
Iф
При несимметричной нагрузке фазные токи и фазовые углы между фазными токами и фазными напряжениями в общем случае не одинаковы.. Линейные токи и в этом случае определяются через соответствующие фазные токи. Векторная диаграмма, построенная для случая несимметричной активной нагрузки трехфазного потребителя при соединении треугольником, представлена на рис. 5.8.
Отключение нагрузки одной из фаз следует рассматривать как частный случай несимметричной нагрузки, когда сопротивление отключённой фазы равно бесконечности.
В этом случае векторная диаграмма приобретает вид, представленный на рис.5.9 (Z = 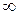 )
)
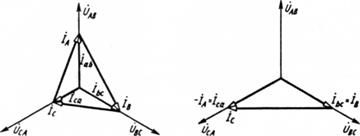
Рис. 5.8 Рис. 5.9
При обрыве линейного провода в цепи трехфазного потребителя электроэнергии, соединенного треугольником, следует рассматривать его как потребителя, подключенного к однофазному источнику (Uab)
Задание по работе
1.Исследовать трехфазную трехпроводную электрическую цепь при соединении потребителей звездой и установить соотно- шения между линейными и фазными токами I л I ф и напряжениями U л U ф при симметричном и несимметричном режимах работы.
2. Исследовать трехфазную четырехпроводную цепь при соединении потребителей звездой и установить соотношения между линейными и фазными токами и напряжениями при симметричном и несимметричном режимах работы.
3. Исследовать трехфазную цепь при соединении потребителей треугольником и установить соотношения между линейными и фазными токами и напряжениями.
4. Для исследуемых цепей построить векторные диаграммы токов и напряжений U при симметричном и несимметричном режимах работы.
5. Составить выводы по работе.
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 718; Нарушение авторских прав?; Мы поможем в написании вашей работы!