
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Докажите что подобные матрицы имеют одинаковые характеристические многочлены
|
|
|
|
Рассмотрим подобные матрицы A и B = C−1AC, где C - невырожденная матрица. Тогда
fB = |B −λE| = |C−1AC −λE| = |C−1AC −C−1(λE)C| = |C−1(A−λE)C| = |A−λE| = fA
Что и требовалось показать.
61. Дайте определение числа Фробениуса неотрицательной квадратной матрицы. Найдите число Фробениуса для матрицы 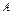 : (а)
: (а) 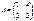 ; (б)
; (б)  . Ответы обоснуйте.
. Ответы обоснуйте.
Числом Фробениуса матрицы A ≥ 0 называется максимальное собственное значение
этой матрицы.
Теорема: Если сумма элементов строки (столбца) матрицы A > 0 одинакова и
равна a, то число Фробениуса матрицы A равно a.
a) матрица  Сумма элементов всех строк равна 5. Следовательно, опираясь на теорему, число Фробениуса этой матрицы равно 5.
Сумма элементов всех строк равна 5. Следовательно, опираясь на теорему, число Фробениуса этой матрицы равно 5.
b) Найдем собственные значения матрицы 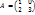
(1-λ)(3-λ) = 0
λ = 1, λ = 3
Числом Фробениуса называется максимальное собственное значение, то есть = 3
62. Дайте определение продуктивной матрицы. Докажите продуктивность матрицы А=(0.2 0.6 0.9 0.3)
Теорема: Матрица A ≥ 0 продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.
Найдем собственные значения матрицы A:
(0.2 − λ)(0.3 − λ) − 0.54 = 0
−0.48 − 0.5λ + λ2 = 0
D = 0.25 + 4 · 0.48 = 0.25 + 1.92 = 2.17
λmax = 0.5+√2.17 /2
√2.17 < 1.5 = √2.25 ⇒ λmax < 0.5+1.5/2 = 1
Число Фробениуса меньше 1, а значит матрица A по определению является продуктивной.
63. Сформулируйте критерий продуктивности матрицы. Приведите пример продуктивной матрицы порядка 3*3
Теорема: Матрица A ≥ 0 продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.
Теорема: Если сумма элементов ∀ строки (∀ столбца) матрицы A > 0 одинакова и равна a, то число Фробениуса матрицы A равно a.
Пример: Рассмотрим матрицу A =
0.2 0.7
0.5 0.4
По теореме (сумма элементов всех строк равна 0.9) число Фробениуса равно λA = 0.9 < 1, а значит (по критерию) рассматриваемая матрица продуктивна.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 887; Нарушение авторских прав?; Мы поможем в написании вашей работы!