Квадратичные формы

64. Дайте определение матрицы квадратичной формы. Найдите матрицу квадратичной формы:

а) ;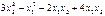

б) .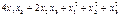

Квадратичной формой Ф от переменных x₁,x₂,…x_n называется однородный многочлен второй степени от этих переменных. Каждая квадратичная форма допускает однозначную запись в следующем симметричном виде:

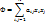
Где a_ij­=a_ji (матрица симметрическая)

Симметрическая матрица А, элементами которой являются числа a_ij, называется матрицей квадратичной формы Ф. Если ввести в рассмотрение столбец X=(x₁;x₂;…;x_n)^T, то квадратичную форму Ф можно записать в матричном виде Ф=X^TAX.

А)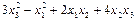

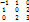
Б)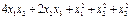

65. Сколько линейно независимых собственных векторов может иметь матрица порядка 3*3

Так как матрица 3 × 3, то характеристический многочлен имеет 3ий порядок, а это значит, что корней (собственных значений матрицы) не более 3, тем более различных действительных корней у многочлена 3ьей степени не более 3.

Теорема (о линейной независимости собственных векторов): Собственные векторы квадратной матрицы, отвечающие различным собственным значениям, линейно независимы.

Следовательно, опираясь на теорему можно утверждать, что действительная симметрическая матрица порядка 3 × 3 имеет не более 3 линейно независимых собственных векторов.

Дата добавления: 2015-03-31