П.1. Простейшие логические символы

Математический анализ. Часть 1.

Литература.

1) А.С. Солодовников, В.А. Бабайцев, А.В.Браилов, И.Г. Шандра. Математика в экономике. – Часть 2. (Издание второе, переработанное и дополненное). – М.: Финансы и статистика, 2005 (и более поздние издания).

2)Сборник задач по курсу «Математика в экономике». Часть 2, математический анализ.

Под редакцией В.А.Бабайцева и В.Б. Гисина. – М.: Финансы и статистика», 2013.

Дополнительная литература.

3) Н.Ш. Кремер. и др. Высшая математика для экономистов. –М.: ЮНИТИ, 1997 и более поздние года.

4) Кудрявцев Л.Д. Курс математического анализа.- 5-е изд. –М.: «Дрофа», 2003,-т.1.

5) Зорич В.А. Курс математического анализа.- 4-е изд. –М.: «МЦНМО», 2002,-ч.1.

6) Фихтенгольц Г.М. Курс интегрального и дифференциального исчисления. Том 1. – М.: Физматлит, 2003

Раздел 1. Введение в анализ: множества, функции.

До XVII века математический анализ представлял собой совокупность решений разрозненных частных задач, например, в интегральном исчислении – это задачи на вычисление площадей фигур, объемов тел с кривыми границами и т.д. Каждая задача решалась своим методом, часто сложным и громоздким. Математический анализ как единое и систематическое целое сложился в трудах И. Ньютона, Г. Лейбница, Л. Эйлера, Ж. Лагранжа и других ученых XVII-XVIII веков, а его база – теория пределов – была разработана О. Коши в начале XIX века. Глубокий анализ исходных понятий математического анализа был связан с развитием в XIX-XX веках теории множеств, теории меры, теории функций действительного переменного и привел к разнообразным обобщениям.

Определение. Высказыванием называется всякое предложение, о котором можно сказать истинно оно или ложно.

Пример. Пусть 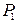- предположение - «Москва – столица РФ». - Это истинное высказывание. (и).

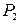- «Каждый студент нашего университета - отличник». - Это ложное высказывание. (л)

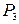- «Треугольник Х – равносторонний». - Не высказывание.

Не всякое предположение является высказыванием, например, определение не является высказыванием.

Дата добавления: 2015-03-31