Теоретический материал. Тема: Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей

Тема: Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей

Практическая работа №8

Критерии оценки практических работ

Общие требования к оформлению и выполнению практических работ

Форма отчетности:

1. работы требуется выполнять в отдельной тетради для практических работ;

2. каждая работа должна содержать:

- номер и название практической работы;

- цель работы;

- условия заданий;

- подробное решение заданий.

«5» -работа выполнена в заданное время, самостоятельно, с соблюдением последовательности, качественно и творчески;

«4» - работа выполнена в заданное время, самостоятельно, с соблюдением последовательности, при выполнении отдельных операций допущены небольшие отклонения;

«3» - работа выполнена в заданное время, самостоятельно, с нарушением последовательности, отдельные операции выполнены с отклонением от образца (если не было на то установки); работа оформлена небрежно или не закончена в срок;

«2» – студент самостоятельно не справился с работой, последовательность нарушена, при выполнении операций допущены большие отклонения, работа оформлено небрежно и имеет незавершенный вид.

Цель: Формирование навыков вычисления пределов с помощью замечательных пределов, раскрытия неопределенностей

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Число 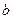называется пределом функци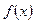и при 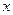, стремящемся к 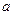, если для любого числа найдется такое число 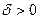, что при всех 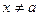, удовлетворяющих неравенству , будет выполнено неравенство .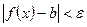

Вычисление предела функции 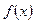следует начинать с подстановки предельного значения аргумента 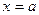, ( 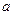- число или один из символов 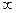, , 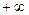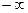) в выражение, определяющее эту функцию. При этом приходится сталкиваться с двумя существенно различными типами примеров.

I. Если основная элементарная функция определена в предельной точке 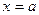, то .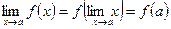

Имеют место основные теоремы, на которых основано вычисление пределов элементарных функций.

1. Если 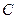- постоянная величина, то .

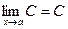2. Если 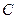- постоянная величина, то .

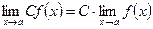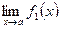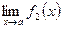3. Если существуют конечные пределы и , то:

;

;

.

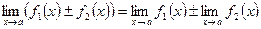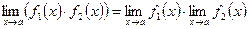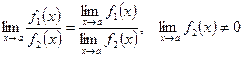II. Функция 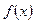в предельной точке 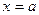не определена. Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях (наиболее простых) вопрос сводится к применению теорем о свойствах бесконечно малых и бесконечно больших функций и связи между ними.

Более сложными случаями нахождения предела являются такие, когда подстановка предельного значения аргумента в выражение для 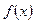приводит к одной из неопределенностей:

, , , , , , .

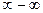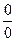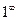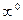Тогда вычисление предела заключается в раскрытии полученных неопределенностей.

Здесь могут оказаться полезными:

первый замечательный предел 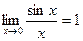, ( 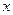- радианная мера угла);

второй замечательный предел .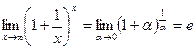

Кроме того, при раскрытии неопределенностей используют следующие приемы:

1. сокращение дроби на критический множитель при ;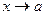

2. избавление от иррациональности в числителе или знаменателе дроби;

3. разложение многочленов на линейные или квадратичные множители при , .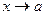

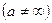Дата добавления: 2015-03-31