
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практическая работа №10. Задание 1: Вычислите односторонние пределы: 1) ;
|
|
|
|
Пример
Задание 1: Вычислите односторонние пределы: 1) 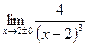 ;
;
2) 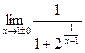 .
.
Решение: 1) Пусть 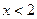 . Тогда при
. Тогда при 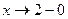 функция
функция 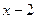 , а, следовательно, и
, а, следовательно, и 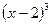 есть отрицательная бесконечно малая, поэтому функция
есть отрицательная бесконечно малая, поэтому функция 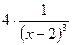 - отрицательная бесконечно большая, то есть
- отрицательная бесконечно большая, то есть 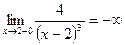 .
.
При 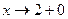 функция
функция 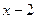 , а, следовательно, и
, а, следовательно, и 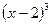 - положительная бесконечно большая функция, то есть
- положительная бесконечно большая функция, то есть 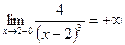 .
.
2) Пусть 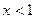 . Тогда при
. Тогда при 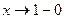 имеем:
имеем: 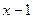 - отрицательная бесконечно малая функция; следовательно,
- отрицательная бесконечно малая функция; следовательно, 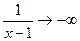 и
и 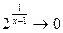 . Отсюда
. Отсюда 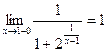 .
.
Если 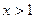 , то при
, то при 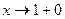 получим:
получим: 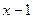 - положительная бесконечно малая функция; следовательно,
- положительная бесконечно малая функция; следовательно, 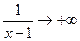 и
и 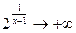 , тогда
, тогда 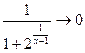 . Имеем,
. Имеем, 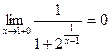 .
.
Задание 2: Даны функции: 1) 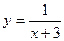 ; 2)
; 2) 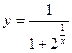 . Найти точки разрыва и исследовать их характер.
. Найти точки разрыва и исследовать их характер.
Решение: 1) Функция 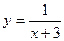 определена при всех значениях
определена при всех значениях 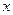 , кроме
, кроме 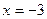 . Так как эта функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков
. Так как эта функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков 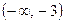 и
и 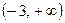 .
.
Следовательно, единственной точкой разрыва является точка 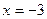 (функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней неопределена). Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке разрыва
(функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней неопределена). Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке разрыва 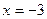 :
: 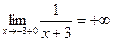 ,
, 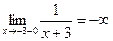 .
.
Следовательно, при 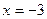 функция
функция 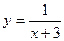 имеет бесконечный разрыв;
имеет бесконечный разрыв; 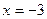 есть точка II рода.
есть точка II рода.
2) Рассуждая аналогично, получим, что точкой разрыва заданной функции является  . Найдем односторонние пределы этой функции в точке
. Найдем односторонние пределы этой функции в точке  :
: 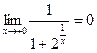 ,
, 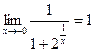 .
.
Таким образом, левый и правый пределы исследуемой функции при  конечны, но не равны между собой. Поэтому
конечны, но не равны между собой. Поэтому  точка I рода, причем точка скачка функции.
точка I рода, причем точка скачка функции.
Задания для практической работы
1. Вычислите односторонние пределы:
1) 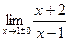 ; 2)
; 2) 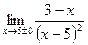 ; 3)
; 3) 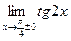 ;
;
4) 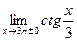 ; 5)
; 5) 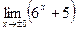 ; 6)
; 6) 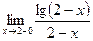 .
.
2. Для данных функций найдите точки разрыва и исследуйте их характер:
1) 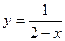 ; 2)
; 2) 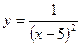 ; 3)
; 3) 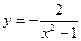 ;
;
4) 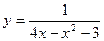 ; 5)
; 5) 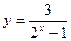 ; 6)
; 6) 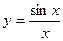 .
.
3. Исследуйте на непрерывность функции:
1) 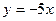 ; 2)
; 2) 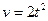 ; 3)
; 3) 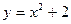 ;
;
4) 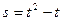 ; 5)
; 5) 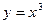 ; 6)
; 6) 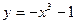 .
.
Вопросы для самоконтроля:
1. Дайте определение непрерывной функции.
2. Что называется точкой разрыва?
3. На какие два типа делятся точки разрыва? Дайте определение.
4. Какие пределы называются односторонними?
5. Какая точка называется точкой устранимого разрыва?
6. Какая точка называется точкой скачка? Что называется скачком?
Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 2.2, 2.3, 2.4, 2.5
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 686; Нарушение авторских прав?; Мы поможем в написании вашей работы!